Blog
2023-03-14
A circle of radius \(r\) on a piece of paper can be thought of as a line through all the points on the paper that are a distance \(r\) from the centre of the circle.
The length of this line (ie the circumference) is \(2\pi r\).
Due to the curvature of the Earth, the line through all the points that are a distance \(r\) from where you are currently standing will be less than \(2\pi r\) (although you might
not notice the difference unless \(r\) is very big). The type of curvature that a sphere has is often called positive curvature.
It is also possible to create surfaces that have negative curvature; or surfaces where the length of the line through all the points that are a distance \(r\) from a point is more than \(2\pi r\).
These surfaces are called hyperbolic surfaces.
Hyperbolic surfaces
The most readily available example of a hyperbolic surface is a Pringle: Pringles are curved upwards in one direction, and curved downwards in the other direction.
It's not immediately obvious what a larger hyperbolic surface would look like, but you can easily make one if you know how to crochet: simply increase the number of stitches at a
constant rate.
If it was possible to continue crocheting forever, you'd get an unbounded hyperbolic surface: the hyperbolic plane.
Over the last few weeks, I've been working on adding hyperbolic levels to Mathsteroids, the asteroids-inspired game that I started making levels for in 2018.
There are quite a few different ways to represent the hyperbolic plane in 2D. In this blog post we'll take a look at some of these; I encourage you to play the Mathsteroids level for each one as you
read so that you can get a feeling for their behaviour.
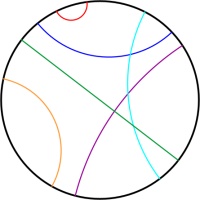
Poincaré disk
The Poincaré disk represents the hyperbolic plane as the interior of a circle. As objects move away from the centre of the circle, they appear smaller and smaller; and the circumference of
the circle is infinitely far from the centre of the circle. Straight lines on the hyperbolic plane appear on the Poincaré disk as either circles that meet the edge of the disk at right angles,
or straight lines through the centre of the circle.
One of the nicest properties of the Poincaré disk is that it correctly represents angles: If you measure the angle between to intersecting straight lines represented on the disk, then the value
you measure will be the same as the angles between the two lines in the actual hyperbolic plane.
This representation can be used to demonstrate some interesting properties of the hyperbolic plane.
In normal two dimensional space, if you are given a line and a point then there is exactly one line that goes through the point and is parallel to the first line.
But in hyperbolic space, there are many such parallel lines.
In Mathsteroids, there are two levels based on the Poincaré disk. The first level is bounded: you can only fly so far from the centre of the circle before
you hit the edge of the level and bounce back. (This prevents you from getting lost in the part of the disk where you would appear very very small.)
The second level is unbounded. In this level, you can fly as far as you like in any direction, but the point which is at the centre of the
disk will change when you go too far to prevent the ship from getting to small.
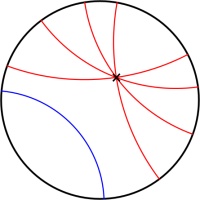
Beltrami–Klein disk
Simlar to the Poincaré disk, the Beltrami–Klein disk represents the hyperbolic plane using the interior of a circle, with the edge of the circle infinitely far away. Straight lines
in hyperbolic space will appear as straight lines in the Beltrami–Klein disk. The Beltrami–Klein disk is closely related to the Poincaré disk: the same line represented on both disks
will have its endpoints at the same points on the circle (although these endpoints are arguably not part of the line as they are on the circle that is infinitely far away).
Unlike in the Poincaré disk, angles are not correctly represented in the Beltrami–Klein disk. It can however be a very useful representation as straight lines appearing as straight lines
is a helpful feature.
Again, there are two Mathsteroids levels based on the Beltrami–Klein disk: a bounded level and an unbounded level.
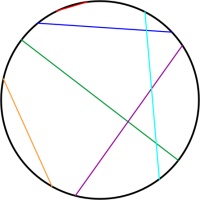
Poincaré half-plane
The Poincaré half-plane represents the hyperbolic plane using the half-plane above the \(x\)-axis. Straight lines in hyperbolic space are represented by either vertical
straight lines or semicircles with their endpoints on the \(x\)-axis.
Like the Poincaré disk, the Poincaré half-plane correctly represents the angles between lines.
There is one Mathsteroids level based on the Poincaré half-plane: this level is bounded so you can only travel so far away from where you start.
Band
The band representation represents the hyperbolic plane as the strip between two horizontal lines. The strip extends forever to the left and right.
Straight lines on the band come in a variety of shapes.
There is one Mathsteroids level based on the band representation: the bounded level.
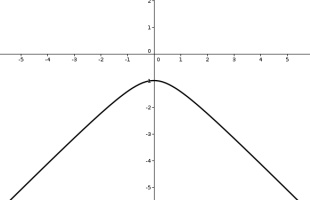
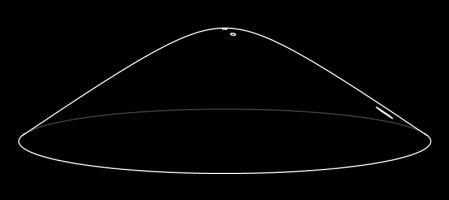
Hyperboloid and Gans plane
The hyperbolic plane can be represented on the surface of a hyperboloid. A hyperboloid is the shape you get if you rotate and hyperbola (a curve shaped like \(y=1/x\).)
Straight lines on this representation are the intersections of the hyperboloid with flat planes that go through the origin.
You can see what these straight lines look like by playing the (bounded) Mathsteroids level based on the hyperboloid.
The Gans plane is simply the hyperboloid viewed from above. There is a (bounded) Mathsteroids level based on the Gans plane.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2023-02-03
Imagine a set of 142 points on a two-dimensional graph.
The mean of the \(x\)-values of the points is 54.26.
The mean of the \(y\)-values of the points is 47.83.
The standard deviation of the \(x\)-values is 16.76.
The standard deviation of the \(y\)-values is 26.93.
What are you imagining that the data looks like?
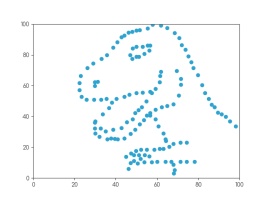
Whatever you're thinking of, it's probably not this:
This is the datasaurus, a dataset that was created by Alberto Cairo in
2016 to remind people to look beyond the summary statistics when analysing a dataset.
Anscombe's quartet
In 1972, four datasets with a similar aim were publised. Graphs in statistical analysis by Francis J Anscombe [1] contained four datasets that have become known as Anscombe's quartet: they all have the same
mean \(x\)-value, mean \(y\)-value, standard deviation of \(x\)-values, standard deviation of \(y\)-values, linear regression line, as well multiple other values
related to correlation and variance. But if you plot them, the four datasets look very different:
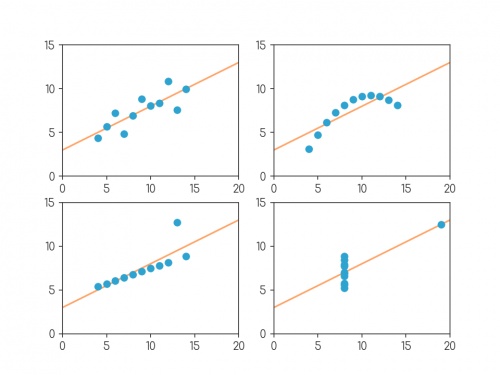
Plots of the four datasets that make up Anscombe's quartet. For each set of data:
the mean of the \(x\)-values is 9; the mean of the \(y\)-values is 7.5;
the standard deviation of the \(x\)-values is 3.32; the standard deviation of the \(y\)-values is 2.03;
the correlation coefficient between \(x\) and \(y\) is 0.816;
the linear regression line is \(y=3+0.5x\);
and coefficient of determination of linear regression is 0.667.
Anscombe noted that there were prevalent attitudes that:
- "Numerical calculations are exact, but graphs are rough."
- "For any particular kind of statistical data, there is just one set of calculations constituting a correct statistical analysis."
- "Performing intricate calculations is virtuous, actually looking at the data is cheating."
The four datasets were designed to counter these by showing that data exhibiting the same statistics can actually be very very different.
The datasaurus dozen
Anscombe's datasets indicate their point well, but the arrangement of the points is very regular and looks a little artificial when compared with real data sets.
In 2017, twelve sets of more realistic-looking data were published (in Same stats, different graphs: generating datasets with varied appearance and identical statistics through simulated annealing by Justin Matejka and George Fitzmaurice [2]).
These datasets—known as the datasaurus dozen—all had the same
mean \(x\)-value, mean \(y\)-value,
standard deviation of \(x\)-values, standard deviation of \(y\)-values, and corellation coefficient (to two decimal places) as the datasaurus.
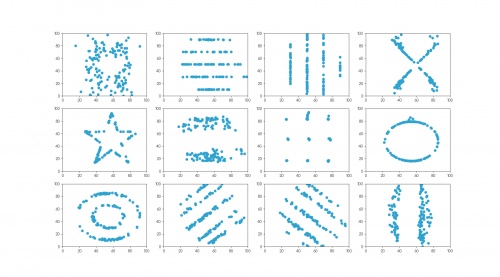
The twelve datasets that make up the datasaurus dozen. For each set of data (to two decimal places):
the mean of the \(x\)-values is 54.26; the mean of the \(y\)-values is 47.83;
the standard deviation of the \(x\)-values is 16.76; the standard deviation of the \(y\)-values is 26.93;
the correlation coefficient between \(x\) and \(y\) is -0.06.
Creating datasets like this is not trivial: if you have a set of values for the statistical properties of a dataset, it is difficult to create a dataset with those properties—especially
one that looks like a certain shape or pattern.
But if you already have one dataset with the desired properties, you can make other datasets with the same properties by very slightly moving every point in a random direction then
checking that the properties are the same—if you do this a few times, you'll eventually get a second dataset with the right properties.
The datasets in the datasaurus dozen were generated using this method: repeatedly adjusting all the points ever so slightly, checking if the properties were the same, then
keeping the updated data if it's closer to a target shape.
The databet
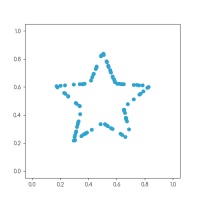
Using the same method, I generated the databet: a collection of datasets that look like the letters of the alphabet. I started with this set
of 100 points resembling a star:
After a long time repeatedly moving points by a very small amount, my computer eventually generated these 26 datasets, all of which have the same means,
standard deviations, and correlation coefficient:
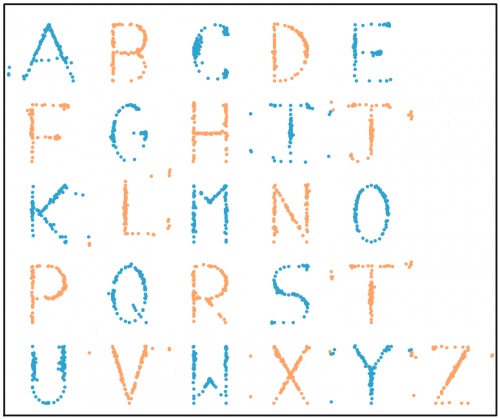
The databet. For each set of data (to two decimal places):
the mean of the \(x\)-values is 0.50; the mean of the \(y\)-values is 0.52;
the standard deviation of the \(x\)-values is 0.17; the standard deviation of the \(y\)-values is 0.18;
the correlation coefficient between \(x\) and \(y\) is 0.16.
Words
Now that we have the alphabet, we can write words using the databet. You can enter a word or phrase here to do this:
Given two data sets with the same number of points, we can make a new larger dataset by including all the points in both the smaller sets.
It is possible to write the mean and standard deviation of the larger dataset in terms of the means and standard deviations of the smaller sets: in each case,
the statistic of the larger set depends only on the statistics of the smaller sets and not on the actual data.
Applying this to the databet, we see that the datasets that spell words of a fixed length will all have the same mean and standard deviation.
(The same is not true, sadly, for the correlation coefficient.) For example, the datasets shown in the following plot both have the same means and standard deviations:

Datasets that spell "TRUE☆" and "FALSE". For both sets of (to two decimal places):
the mean of the \(x\)-values is 2.50; the mean of the \(y\)-values is 0.52;
the standard deviation of the \(x\)-values is 1.42; the standard deviation of the \(y\)-values is 0.18.
Hopefully by now you agree with me that Anscombe was right: it's very important to plot data as well as looking at the summary statistics.
If you want to play with the databet yourself, all the letters are available on GitHub in JSON format.
The GitHub repo also includes fonts that you can download and install so you can use Databet Sans in
your next important document.
References
[1] Graphs in statistical analysis by Francis J Anscombe. American Statistician, 1973.
[2] Same stats, different graphs: generating datasets with varied appearance and identical statistics through simulated annealing by Justin Matejka and George Fitzmaurice. Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, 2017.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2023-01-08
Welcome to 2023 everyone! Now that the Advent calendar has disappeared, it's time to reveal the answers and announce the winners.
But first, some good news: with your help, the drones were all destroyed in time for Santa to deliver presents and Christmas was saved!
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar and a couple of other interesting bits and pieces.
Highlights
My first highlight is the puzzle from 1 December. I like this puzzle, because the lines of symmetry of a rectangle that you might expect—although it's not too hard to
see what the lines of symmetry are, so this makes a nice gentle first puzzle.
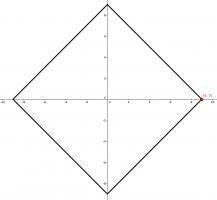
1 December
One of the vertices of a rectangle is at the point \((9, 0)\). The \(x\)-axis and \(y\)-axis are both lines of symmetry of the rectangle.
What is the area of the rectangle?
My next hightlight is the puzzle from 11 December. I always enjoy a surprise appearance of the Fibonacci sequence.
11 December
There are five 3-digit numbers whose digits are all either 1 or 2 and who do not contain
two 2s in a row: 111, 112, 121, 211, and 212.
How many 14-digit numbers are there whose digits are all either 1 or 2 and who do not contain
two 2s in a row?
My next highlight is the puzzle from 13 December. I love a good crossnumber, and had a lot of fun making this small one up. (If you enjoyed this one, you should check out the
crossnumbers I write for Chalkdust.)
13 December
Today's number is given in this crossnumber. The across clues are given as normal, but the down clues are given in a random order: you must work out
which clue goes with each down entry and solve the crossnumber to find today's number.
No number in the completed grid starts with 0.
|
|
| |||||||||||||||||||||||||
My final highlight is the puzzle from 24 December. You could solve this by doing a lot of expanding, but there's a neat shortcut that makes it almost trivial to solve.
24 December
The expression \((3x-1)^2\) can be expanded to give \(9x^2-6x+1\). The
sum of the coefficients in this expansion is \(9-6+1=4\).
What is the sum of the coefficients in the expansion of \((3x-1)^7\)?
Hardest and easiest puzzles
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
You can see that the most difficult puzzles were those on
11,
18 and
19 December;
and the easiest puzzle was on
8 December.
The winners
And finally (and maybe most importantly), on to the winners: 192 people managed to destroy all three drones. That's more people than last year:
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
| Year | |||||||
From the correct answers, the following 10 winners were selected:
- Claire Metcalfe
- Shivanshi
- Gary M
- Katharine Velleman
- James Dolengewicz
- Cathy Hooper
- Alan Buck
- Yurie Ito
- Kai
- Nicholas Jackson
Congratulations! Your prizes will be on their way shortly.
The prizes this year include 2022 Advent calendar T-shirts. If you didn't win one, but would like one of these, I've made them available to buy at merch.mscroggs.co.uk alongside the T-shirts from previous years.
Additionally, well done to
Aaron Johnson, Aaron Stiff, Aidan Dodgson, Alejandro Villarreal, Alek2ander, Alex Bolton, Alex Davis, Alex Hartz, Andrew Brady, Andrew Brodie, Andrew Ennaco, Andrew Roy, Andrew Turner, Artie Smith, Ashton Lewis, Austin Antoniou, Becky Russell, Ben Baker, Ben Boxall, Ben Reiniger, Ben Tozer, Ben Weiss, Beth Jensen, Blake, Brennan Dolson, Brian Carnes, Brian Wellington, Carl Westerlund, Carmen, Charleston W, Chris Eagle, Chris Hellings, Colin Beveridge, Colin Brockley, Connie, Corbin Groothuis, CreativeCrocheter, Dan Colestock, Dan DiMillo, Dan May, Dan Swenson, Dan Whitman, Daniel Cuneo, David and Ivy Walbert, David Ault, David Berardo, David Fox, David Kendel, David Mitchell, Deborah Tayler, Deborah Tayler, Derek Perrin, Dominik Niemand, Don Anderson, Dr Lizzie, Duncan Schaafsma, Dylan Richard, Eleanor, Elizabeth Blackwell, Elizabeth Madisetti, Emilie Heidenreich, Emily Troyer, Emma, Eoin Davey, Eric Kolbusz, Eric Scotti, Erik Eklund, Fionn Woodcock, Frances, Frank Kasell, Fred Verheul, Freddie Mao, Félix Breton, Gabriella Pinter, Gary M. Gerken, Gerry, Gert-Jan, Greg W., Gregory Loges, Greta, Han Whiteoak, Hannah Charman, Heerpal Sahota, Helen F, Herschel, Iris, Jack, Jacob, Jacob Loader, James Chapman, James Cunnane, Jarvis9, Jean-Noël Monette, Jean-Sébastien Turcotte, Jen Sparks, Jessica Marsh, Jim Ashworth, Jon Palin, Jonathan Chaffer, Jonathan Thiele, Jorge del Castillo Tierz, Joseph Gage, Joseph Wagner, Joshua Park, Karen Climis, Kevin Docherty, Kirsty Fish, Kristen Koenigs, Kyle Allen, Lazar Ilic, Lewis Dyer, Lise Andreasen, Louis, LycanFayn, Lyra, Magnus Eklund, Marco van der Park, Mark Stambaugh, Martin Harris, Martin Holtham, Mathryn, Matt Thomson, Mels, Merrilyn, Michael DeLyser, Mihai Zsisku, Mike L, Mike R, Millie, Mr J Winfield, Nadine Chaurand, Nancy Walker, Naomi Bowler, Naomi C, Nick Keith, Niji Ranger, Pamela Docherty, Patrick, Philip Corradi, Priyesh, Pup, Qaysed, Qaysed, Rashi, Ray Arndorfer, Reid, Reuben, Riccardo Lani, Rob Dixon, Robert Brady, Roger Lipsett, Roni Malek, Rosie Paterson, Russ Collins, Ruth Franklin, Sage Robinson, Sam Drei, Sarah Brook, Scott, Sean Henderson, Seth Cohen, shadorfff, Simon English, Stephen Cappella, Stephen Jasina, Sumaya Felic, Tamara Brenner, Tarim, The Connors of York, The Steelblade, Tom Fryers, Tony Mann, tripleboleo, Tyler St Clare, UsrBinPRL, Valentin VĂLCIU, Vinayak, Vinny R, vortex, Yasha, Yuliya N., and Zoran Morrissey-Ralevic.
who all also completed the Advent calendar but were too unlucky to win prizes this time or chose to not enter the prize draw.
See you all next December, when the Advent calendar will return.
Edit: Removed myself (and a second copy of myself) from the list of solvers.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
You didn't mention the rate limiting you put in for the bots!
Sorry about that
Sorry about that
(anonymous)
I fought very hard to solve the middle "here are the 6 answers, construct the 6 small problems", but I just couldn't. Hints about that one and the genre in general would be great.
Lise Andreasen
@Valentin V?LCIU: Oops, forgot to remove my testing that everything works from the list of people! (Removing it now)
Matthew
Add a Comment
2022-12-29
This is the 100th blog post on this website!
But if I hadn't pointed this out,
you might not have noticed: the URL of the page is mscroggs.co.uk/blog/99 and not mscroggs.co.uk/blog/100.
This is a great example of an off-by-one error.
Off-by-one errors are one of the most common errors made when programming and elsewhere, and this is an excellent opportunity to blog about them.
Fence posts and fence panels
Imagine you want to make a straight fence that is 50m long. Each fencing panel is 2m long.
How many fence posts will you need?
Have a quick think about this before reading on.
If you're currently thinking about the number 25, then you've just made an off-by-one error.
The easiest way to see why is to think about some shorter fences.
If you want to make a fence that's 2m long, then you'll need just one fence panel. But one fence
post will not be enough: you'll need a second post to put at the other end of the fence panel.
If you want to make a 4m long fence, you'll need a post before the first panel, a post between
the two panels, and a post after the second panel: that's three posts in total.
In general, you'll always need one more fence post than panel, as you need a fence post
at the start of each panel and an extra post at the end of the final panel.
(Unless, of course, you're building a fence that is a closed loop.)
This fence post/fence panel issue appears surprisingly often, and can make counting things
quite difficult. For example, the first blog post
on this website was posted in 2012: ten years ago. But if you count the number of years listed in the
archive there are 11 years. If you release an issue of a magazine once a year, then issue 11 (not issue 10) will
be the issue released 10 years after you start not issue 10. If, like Chalkdust,
you release issues two times a year, issue 21 (not issue 20) will be the 10 year issue.
Half-open intervals
An interval is called closed if it includes its starting and ending point, and open if it
doesn't include them. A half-open interval includes one end point and not the other.
Using half-open intervals makes counting things less difficult: including one endpoint but not the other is a bit like ignoring
the final (or first) fence post so that there are the same number of post and panels.
In Python, the range function includes the first number but not the last
(this is the sensible choice as including the final number and not the first would be very confusing).
range(5, 8) includes the numbers 5, 6, and 7 (but not 8).
By excluding the final number, the number of numbers in a range
will be equal to the difference between the two input numbers.
Excluding the final item so that the number of items in a range is equal to the difference between the start and end is a great way to
reduce opportunities for off-by-one errors, and isn't too hard to get used to.
Why start at 0?
We've seen a couple of causes of off-by-one errors, but we've not yet seen why this page's URL
contains 99 rather than 100. This is because the numbering of blog posts started at zero.
But why is it a sensible choice to start at 0?
Using a half-open range, the first \(n\) numbers starting at 1 would be range(1, n + 1); the first \(n\) numbers starting at 0 on the other hand
would be range(0, n). The second option is neater, as you don't have to add one to the final number; the first option opens up more opportunities for
off-by-one errors.
This is one of the reasons why Python and many other programming languages start their numbering from 0.
Why doesn't everyone start at 0?
Starting at 0 and using half-open intervals to represent ranges of integers seem like good ways to help people avoid making off-by-one errors, but this choice is not perfect.
If you want to write a range of numbers from 1 to 8 inclusive using this convention, you would have to write range(1, 9):
forgetting to add one to the final number in this situation is another source of off-by-one errors.
It's also more natural to many people to start counting from 1, so some programming languages choose different conventions. The following table sums up the different possible
conventions, which desirable properties they have, and which languages use them.
| Convenction | Languages using this convention | Length of range is difference between endpoints | range(START, n) contains \(n\) numbers | range(START, n) contains START | range(START, n) contains \(n\) |
| START=0, range includes first endpoint only | Python, Javascript, PHP, Rust, C, C++ | ✓ | ✓ | ✓ | ✗ |
| START=0, range includes last endpoint only | ✓ | ✓ | ✗ | ✓ | |
| START=0, range includes both endpoints | ✗ | ✗ | ✓ | ✓ | |
| START=0, range includes neither endpoint | ✗ | ✗ | ✗ | ✗ | |
| START=1, range includes first endpoint only | ✓ | ✗ | ✓ | ✗ | |
| START=1, range includes last endpoint only | ✓ | ✗ | ✗ | ✓ | |
| START=1, range includes both endpoints | Matlab, Julia, Fortran | ✗ | ✓ | ✓ | ✓ |
| START=1, range includes neither endpoint | ✗ | ✗ | ✗ | ✗ |
(I don't know of any languages that use any of the other conventions, but if you have please let me know in the comments below and I'll add them.)
None of the conventions manages to remove all the possible sources of confusion, so it looks like off-by-one errors are here to stay.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Hi!!!
Love your blog posts!
They make me get out of bed in the morning.
Just wanted to show my appreciation.
Cheers.
Love your blog posts!
They make me get out of bed in the morning.
Just wanted to show my appreciation.
Cheers.
Anonymous#3728
Add a Comment
2022-12-04
In November, I spent some time (with help from TD) designing this year's Chalkdust puzzle Christmas card.
The card looks boring at first glance, but contains 11 puzzles. By colouring in the answers to the puzzles on the front of the card in black (each answer appears twice), then colouring remaining squares
containing 0s red, and regions containing a star brown,
you will reveal a Christmas themed picture.
If you want to try the card yourself, you can download this printable A4 pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will automatically be found and coloured in black, and appropriate squares and regions will be coloured red and brown...
The puzzles | ||
| 1. | What is the only prime number that is both two more than a prime number and two less than a prime number? | Answer |
| 2. | Holly adds up the first 7 odd numbers. What total does she get? | Answer |
| 3. | Holly next adds up the first \(n\) odd numbers to get a total of 1089. What is \(n\)? | Answer |
| 4. | Ivy starts with 0 then adds or subtracts some multiples of 4 or 7. What is the smallest positive integer that she could have ended with? | Answer |
| 5. | Ivy again starts with 0, but this time she adds or subtracts some multiples of 240 or 400. What is the smallest positive integer that she could have ended with? | Answer |
| 6. | How many 4-digit integers are there whose digits are all non-zero and whose digits add up to 7? | Answer |
| 7. | How many positive integers are there whose digits are all non-zero and whose digits add up to 7? | Answer |
| 8. | Eve wrote down a four-digit number. Eve then removed one of the digits of her number to make a three-digit number. The sum of her two numbers is 3119. What was her four-digit number? | Answer |
| 9. | Eve wrote down a five-digit number. Eve then removed one of the digits of her number to make a four-digit number. The sum of her two numbers is 96158. What is the largest number that her five-digit number could have been? | Answer |
| 10. | Noel drew 12 points on the circumference of a circle, then drew a straight line connecting every pair of points. How many lines did he draw? | Answer |
| 11. | Noel drew some points on the circumference of a circle, then drew a straight line connecting every pair of points. He drew 2926 lines. How many points did he draw? | Answer |
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Great fun thanks. At first they seem impossible but then a way through appears! How do I get the answers / check if I’m right?
Graeme Johnston
Add a Comment