Blog
2020-05-15
This is a post I wrote for The Aperiodical's Big Lock-Down Math-Off. You can vote for (or against) me here until 9am on Sunday...
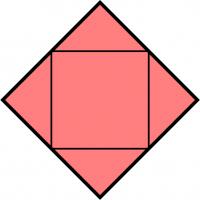
Recently, I came across a surprising fact: if you take any quadrilateral and join the midpoints of its sides, then you will form a parallelogram.
![](javascript:showlimage("parallelograms.png"))
The blue quadrilaterals are all parallelograms.
The first thing I thought when I read this was: "oooh, that's neat." The second thing I thought was: "why?" It's not too difficult to show why this is true; you might like to pause here and try to work out why yourself before reading on...
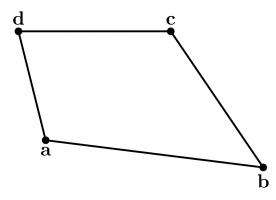
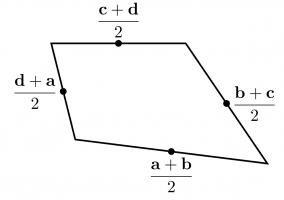
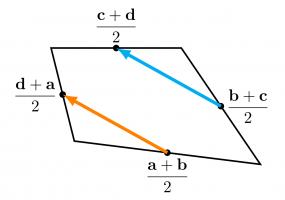
To show why this is true, I started by letting \(\mathbf{a}\), \(\mathbf{b}\), \(\mathbf{c}\) and \(\mathbf{d}\) be the position vectors of the vertices of our quadrilateral. The position vectors of the midpoints of the edges are the averages of the position vectors of the two ends of the edge, as shown below.
![](javascript:showlimage("quadproof1.png"))
![](javascript:showlimage("quadproof2.png"))
The position vectors of the corners and the midpoints of the edges.
We want to show that the orange and blue vectors below are equal (as this is true of opposite sides of a parallelogram).
![](javascript:showlimage("quadproof3.png"))
We can work these vectors out: the orange vector is$$\frac{\mathbf{d}+\mathbf{a}}2-\frac{\mathbf{a}+\mathbf{b}}2=\frac{\mathbf{d}-\mathbf{b}}2,$$
and the blue vector is$$\frac{\mathbf{c}+\mathbf{d}}2-\frac{\mathbf{b}+\mathbf{c}}2=\frac{\mathbf{d}-\mathbf{b}}2.$$
In the same way, we can show that the other two vectors that make up the inner quadrilateral are equal, and so the inner quadrilateral is a parallelogram.
Going backwards
Even though I now saw why the surprising fact was true, my wondering was not over. I started to think about going backwards.
It's easy to see that if the outer quadrilateral is a square, then the inner quadrilateral will also be a square.
![](javascript:showlimage("quad-sqsq.png"))
If the outer quadrilateral is a square, then the inner quadrilateral is also a square.
It's less obvious if the reverse is true: if the inner quadrilateral is a square, must the outer quadrilateral also be a square? At first, I thought this felt likely to be true, but after a bit of playing around, I found that there are many non-square quadrilaterals whose inner quadrilaterals are squares. Here are a few:
![](javascript:showlimage("square_shapes.png"))
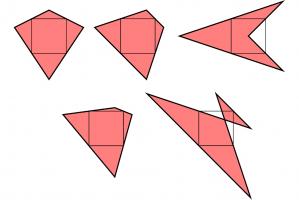
A kite, a trapezium, a delta kite, an irregular quadrilateral and a cross-quadrilateral whose innner quadrilaterals are all a square.
There are in fact infinitely many quadrilaterals whose inner quadrilateral is a square. You can explore them in this Geogebra applet by dragging around the blue point:
As you drag the point around, you may notice that you can't get the outer quadrilateral to be a non-square rectangle (or even a non-square parallelogram). I'll leave you to figure out why not...
×2 ×3 ×2 ×3 ×2(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
mscroggs.co.uk is interesting as far as MATHEMATICS IS CONCERNED!×2 ×3 ×2 ×2 ×4
DEB JYOTI MITRA
×2 ×3 ×2 ×2 ×4 Add a Comment
This is true but it's not needed (it's automatically true), you have in fact already proved that this is a parallelogram, by proving that two opposite sides have same length and are parallel (If you prove that the vectors EF and GH have the same coordinates, then EFHG is a parallelogram.)