Blog
2019-06-19
A308092 The sum of the first \(n\) terms of the sequence is the concatenation of the first \(n\) bits of the sequence read as binary, with \(a(1) = 1\).1, 2, 3, 7, 14, 28, 56, 112, 224, 448, 896, 1791, 3583, 7166, ...

To understand this definition, let's look at the first few terms of this sequence written in binary:
By "the concatenation of the first \(n\) bits of the sequence", it means the first \(n\) binary digits of the whole sequence written in order:
1, then 11, then 110, then 1101, then 11011, then 110111, and so on. So the definition means:
- The first term is 1, as given in the definition (\(a(1)=1\)).
- The sum of the first 2 terms is the first 2 digits: \(1+10=11\).
- The sum of the first 3 terms is the first 3 digits: \(1+10+11=110\).
- The sum of the first 4 terms is the first 4 digits: \(1+10+11+111=1101\).
- The sum of the first 5 terms is the first 5 digits: \(1+10+11+111+1110=11011\).
As we know that the sum of the first \(n-1\) terms is the first \(n-1\) digits, we can calculate the third term of this sequence onwards using:
"\(a(n)\) is the concatenation of the first \(n\) bits of the sequence subtract concatenation of the first \(n-1\) bits of the sequence":
- The third term is \(110 - 11 = 11\).
- The fourth term is \(1101 - 110 = 111\).
- The fourth term is \(11011 - 1101 = 1110\).
- The fifth term is \(110111 - 11011 = 11100\).
The conjecture
Peter's conjecture is that the number of 1s in each term is greater than or equal to the number of 1s in the previous term.
I'm going to prove this conjecture. If you'd like to have a try first, stop reading now and come back when you're ready for spoilers.
(If you'd like a hint, read the next section then pause again.)
Adding a digit
The third term of the sequence onwards can be calculated by subtracting the first \(n-1\) digits from the first \(n\) digits.
If the first \(n-1\) digits form a binary number \(x\), then the first \(n\) digits will be \(2x+d\), where \(d\) is the \(n\)th digit
(because moving all the digits to the left one place in binary is multiplying by two).
Therefore the different is \(2x+d-x=x+d\), and so we can work out the \(n\)th term of the sequence by adding the \(n\)th digit in the
sequence to the first \(n-1\) digits. (Hat tip to Martin Harris, who spotted this first.)
Carrying
Adding 1 to a binary number the ends in 1 will cause 1 to carry over to the left. This carrying will continue until the 1 is carried into
a position containing 0, and after this all the digits to the left of this 0 will remain unchanged.
Therefore adding a digit to
the first \(n-1\) digits can only change the digits from the rightmost 0 onwards.
Endings
We can therefore disregard all the digits before the rightmost 0, and look at how the \(n\)th term compares to the \((n-1)\)th term.
There are 5 ways in which the first \(n\) digits could end:
- \(00\)
- \(010\)
- \(01...10\) (where \(1...1\) is a string of 2 or more ones)
- \(01\)
- \(01...1\) (where \(1...1\) is again a string of 2 or more ones)
We now look at each of these in turn and show that the \(n\)th term will contain at least as many ones at the \((n-1)\)th term.
Case 1: \(00\)
If the first \(n\) digits of the sequence are \(x00\) (a binary number \(x\) followed by two zeros), then the \((n-1)\)th term of the
sequence is \(x+0=x\), and the \(n\)th term of the sequence is \(x0+0=x0\). Both \(x\) and \(x0\) contain the same number of ones.
Case 2: \(010\)
If the first \(n\) digits of the sequence are \(x010\), then the \((n-1)\)th term of the sequence is \(x0+1=x1\),
and the \(n\)th term of the sequence is \(x01+0=x01\). Both \(x1\) and \(x01\) contain the same number of ones.
Case 3: \(01...10\)
If the first \(n\) digits of the sequence are \(x01...10\), then the \((n-1)\)th term of the sequence is \(x01...1+1=x10...0\),
and the \(n\)th term of the sequence is \(x01...10+1=x01...1\). \(x01...1\) contains more ones than \(x10...0\).
Case 4: \(01\)
If the first \(n\) digits of the sequence are \(x01\), then the \((n-1)\)th term of the sequence is \(x+0=x\),
and the \(n\)th term of the sequence is \(x0+1=x1\). \(x1\) contains one more one than \(x\).
Case 5: \(01...1\)
If the first \(n\) digits of the sequence are \(x01...1\), then the \((n-1)\)th term of the sequence is \(x01...1+1=x10...0\),
and the \(n\)th term of the sequence is \(x01...1+1=x10...0\). Both these contain the same number of ones.
In all five cases, the \(n\)th term contains more ones or an equal number of ones to the \((n-1)\)th term, and so the conjecture is true.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-12-28
More than ten correct solutions to this year's Advent calendar puzzle competition were submitted on Christmas Day, so the competition is now over.
(Although you can still submit your answers to get me to check them.) Thank-you to everyone who took part in the puzzle, I've had a lot of
fun watching your progress and talking to you on Twitter, Reddit, etc. You can find all the puzzles and answers (from 1 January) here.
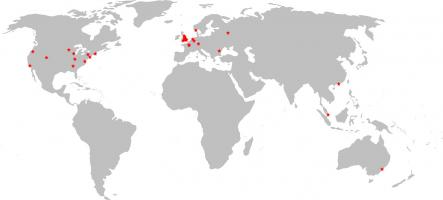
The (very) approximate locations of all the entries I have received so far are shown on this map:
This year's winners have been randomly selected from the 29 correct entries on Christmas Day. They are:
| 1 | Jack Jiang |
| 2 | Steve Paget |
| 3 | Joe Gage |
| 4 | Tony Mann |
| 5 | Stephen Cappella |
| 6 | Cheng Wai Koo |
| 7 | Demi Xin |
| 8 | Lyra |
| 9 | David Fox |
| 10 | Bob Dinnage |
Your prizes will be on their way in early January.
Now that the competition has ended, I can give away a secret. Last year, Neal
suggested that it would be fun if a binary picture was hidden in the answers. So this year I hid one. If you write all the answers in binary, with
each answer below the previous and colour in the 1s black, you will see this:
I also had a lot of fun this year making up the names, locations, weapons and motives for the final murder mystery puzzle. In case you missed them these were:
| # | Murder suspect | Motive |
| 1 | Dr. Uno (uno = Spanish 1) | Obeying nameless entity |
| 2 | Mr. Zwei (zwei = German 2) | To worry others |
| 3 | Ms. Trois (trois = French 3) | To help really evil elephant |
| 4 | Mrs. Quattro (quattro = Italian 4) | For old unknown reasons |
| 5 | Prof. Pum (pum = Welsh 5) | For individual violent end |
| 6 | Miss. Zes (zes = Dutch 6) | Stopping idiotic xenophobia |
| 7 | Lord Seacht (seacht = Irish 7) | Suspect espied victim eating newlyweds |
| 8 | Lady Oito (oito = Portuguese 8) | Epic insanity got him today |
| 9 | Rev. Novem (novem = Latin 9) | Nobody in newsroom expected |
| # | Location | Weapon |
| 1 | Throne room | Wrench (1 vowel) |
| 2 | Network room | Rope (2 vowels) |
| 3 | Beneath reeds | Revolver (3 vowels) |
| 4 | Edge of our garden | Lead pipe (4 vowels) |
| 5 | Fives court | Neighbour's sword (5 vowels) |
| 6 | On the sixth floor | Super banana bomb (6 vowels) |
| 7 | Sparse venue | Antique candlestick (7 vowels) |
| 8 | Weightlifting room | A foul tasting poison (8 vowels) |
| 9 | Mathematics mezzanine | Run over with an old Ford Focus (9 vowels) |
Finally, well done to Scott,
Matthew Schulz,
Michael Gustin,
Daniel Branscombe,
Kei Nishimura-Gasparian,
Henry Hung,
Mark Fisher,
Jon Palin,
Thomas Tu,
Félix Breton,
Matt Hutton,
Miguel,
Fred Verheul,
Martine Vijn Nome,
Brennan Dolson,
Louis de Mendonca,
Roni,
Dylan Hendrickson,
Martin Harris,
Virgile Andreani,
Valentin Valciu,
and Adia Batic for submitting the correct answer but being too unlucky to win prizes this year. Thank you all for taking part and I'll see you
next December for the next competition.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
I got my prize in the mail today. I really liked the stories from Gustave Verbeek; I thought that was pretty clever. I really appreciate you being willing to send the prizes internationally.
Thanks for setting this all up; I had a lot of fun solving the puzzles every day (and solving half them again when my cookie for the site somehow got deleted). I'll be sure to participate next time too!
Thanks for setting this all up; I had a lot of fun solving the puzzles every day (and solving half them again when my cookie for the site somehow got deleted). I'll be sure to participate next time too!
SC
Thanks, Matthew! The puzzles were really fun, and piecing the clues was very interesting too!
Jack
Add a Comment