Blog
2014-06-21
With World Cup fever taking over, you may have forgotten that Wimbledon is just a few days away.
Tennis scoring
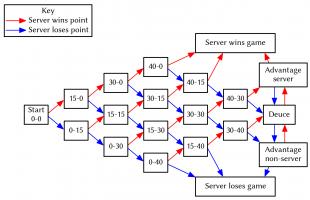
Tennis matches are split into sets (three sets for ladies' matches, five sets for men's), which are in turn split into games. The players take it in turns to serve for a game. The scoring in a game is probably best explained with a flowchart (click to enlarge):
To win a set, a player must win at least six games and two more games than their opponent. If the score reaches six games all, then a tie break is played. In this tie break, the first player to win at least seven points and two points more than their opponent wins. In the final set there is no tie break, so matches can last a long time.
Winning with the smallest share of points
Due to the way tennis is split into sets and games, the player who wins the most points will not necessarily win the match. This got me thinking: what is the smallest proportion of points which can be won while still winning the tennis match?
First, let's consider a men's match. In order to win with the lowest proportion of points, our player should let his opponent win two sets without winning a point and win the other three sets. In the two lost sets, the opponent should win 0-6 taking every point: in total the opponent will win 48 points in these sets.
Leaving the final set for now, the other two sets are won by our player. To win these with the smallest proportion of the points, they should be won 7-6 on a tie break. In the 6 lost games, the opponent should take all the points. In the won games and the tie break, our player should win by two points with the lowest total score. (Winning with more than the lowest total score will mean both players win an equal number of extra points, moving the proportion of points our player wins closer to 50%, higher than it needs to be.)
Therefore, our player will win 4 points out of 6 in the games he wins, win 0 out of 4 points in the games he loses and wins the tie break 7 points to 5. This means that in total our player will 62 points out of 144 in the two won sets.
For the same reason as above, the final set should be won with the lowest total score: 6-4. Using the same scores for each game, our player wins 24 points out of 52.
Overall, our player has won 86 points out of 244, a mere 35% of the points.
If the match is a ladies' match then the same analysis will work, but with each player winning one less set. This gives our player 55 points out of 148, 37% of the points.
This result demonstrates why tennis remains exciting through the whole match. The way tennis is split into sets and games means that our opponent can win 65% of the points but if the pressure gets to them at the most important points, our player can still win the match. This makes for a far more interesting competition than a simple race to one hundred points which could quickly become a foregone conclusion.
Comparing players with serving stats
During tennis matches, players are often compared using statistics such as the percentages of serves which are successful. Imagine a match between Player A and Player B.
In the first set, Player A and Player B are successful with 100% and 92% of their serves respectively. In the second set, these figures are 56% and 48%. Player A clearly looks to be the better server, as they have a higher percentage in each set. However if we look at the two sets in more detail:
| Player A | Player B | |
| First Set | 20/20 | 67/73 |
| Second Set | 45/80 | 13/27 |
| Total | 65/100 | 80/100 |
Table showing successful serves/total serves.
Overall, Player B has an 80% serve success rate, while Player A only manages 65%.
This is an example of Simpson's paradox: a trend which appears in the set-by-set data disappears when the data is combined. This occurs because when we look at the set-by-set percentages, the total number of serves is not taken into account: Player A served more in the second set so their overall percentage will be closer to 56%; Player B served more in the first set so their overall percentage will be closer to 92%.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment