Blog
New machine unfriendly £1 coin
2014-03-19
Vending machines identify coins by measuring their width. Circular coins have the same width in every direction, so designers of vending machines do not need to worry about incorrectly rotated coins causing a blockage or being misidentified. But what about seven-sided 20p and 50p coins?
Perhaps surprisingly, 20p and 50p coins also have a constant width, as show by this video. In fact, the sides of any regular shape with an odd number of sides can be curved to give the shape a constant width.
![](javascript:showlimage("Reuleaux_polygons.png"))
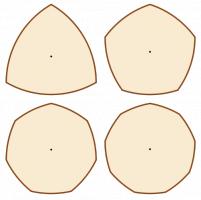
3, 5, 7 and 9 sided shapes of constant width.
Today, a new 12-sided £1 coin was unveiled. One reason for the number of sides was to make the coin easily identified by touch. However, as only polygons with an odd number of sides can be made into shapes of constant width, this new coin will have a different width when measured corner to corner or side to side. This could lead to vending machines not recognising coins unless a new mechanism is added to correctly align the coin before measuring.
Perhaps an 11-sided or 13-sided design would be a better idea, as this would be easily distinguishable from other coins by touch which being a constant width to allow machines to identify it.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment