Blog
2025-06-08
This week, Joel Riley's Every 5×5 Nonogram website
has been doing the rounds. The website includes every nonogram on a 5 by 5 grid that's solvable
without using trial-and-error, and anyone who visits the site can help to solve them all.
At the time of writing, around a quarter of the puzzles have been solved, so if you want to
be part of solving them you'll need to be a bit quick. Be warned though, solving
them can be addictive.
For the uninitiated, a nonogram is a puzzle where you have to colour in some of the squares so that the blocks of coloured squares in each row and column have the sizes given.
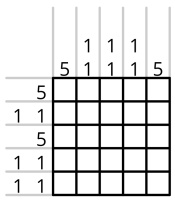
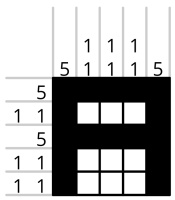
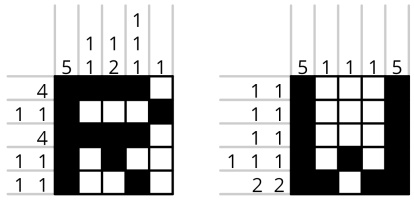
For example, this nongram:
![](javascript:showlimage("a-unfilled.png"))
... has this solution:
![](javascript:showlimage("a-filled.png"))
... because the first column contains one uninterrupted block of 5 black sqaures (5);
the second column contains two non-adjacent blocks of 1 black square (1 1); and so on. If a row or
column is empty, 0 is written in as its clue rather than leaving it blank.
After solving quite a few 5 by 5 nonograms, I started to wonder if I could make solvable nonograms that represented every letter of the alphabet.
Making letters
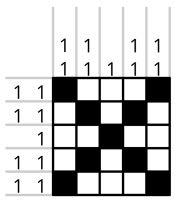
Making an alphabet of nonograms is harder than just drawing each letter, as not all 5 by 5 nonograms have a unique solution. For example, my first attempt to draw the letter X looked like this:
![](javascript:showlimage("x-first-attempt.png"))
But this nonogram has a lot of solutions, including:
![](javascript:showlimage("x-nope.png"))
Checking that a 5×5 nonogram has a unique solution isn't too hard—you can do
this check by trying to solve it then seeing if you get to a point where there's more than one way
to finish—but it would be quite time consuming to do these for all 26 letters, so I wrote
a short Python script to do the checking for me. After a few minutes of tweaking some of the letters,
I had the alphabet.
Making words
Now that I had a nonogram for each letter of the alphabet, I had an idea: I could
use them to make wider nonograms (with a 0 column between them to prevent the letters touching).
Unfortunately, if two 5×5 nonograms both have
unique solutions, it doesn't necessarily follow that the wider nonogram made by putting them together
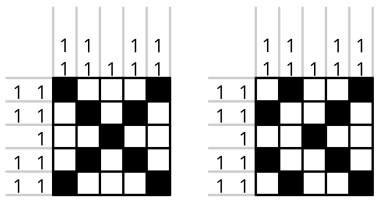
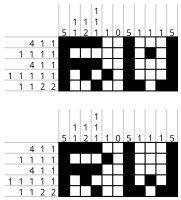
has a unique solution. For example, take the nonograms that were my first candidates for R and W:
![](javascript:showlimage("r-and-w.png"))
There two nonograms both have a unique solution, but if you make a 5×11 nonogram by
placing them next to each other with a 0 column between them, you get a nonogram with multiple
solutions:
![](javascript:showlimage("r-w-fail.png"))
So my first attempt at the alphabet didn't give me a set of nonograms that I could use to spell
words. All was not lost though: after a bit of thinking I came up with an adjusted alphabet that
can be used to spell words and a justification for why any nonogram words built by putting these
letters in a rows will have a unique solution. These are the letters I ended up with:
![](javascript:showlimage("nonogram-alphabet.png"))
If you'd like to make a nonogram for a word or your name, write it in the box below. You can click
on the nonogram that is creates to make it larger:
Why does this alphabet always make solvable words?
To show that this alphabet will always make solvable words, I first looked at every column of
every letter. For many column clues, there are squares that must always be black or always be white:
for example, if the column clue is 5, the squares must all be black; or if a column clue is 3, the
middle square in that column must be black. Looking at my alphabet, you can show that the black and
white squares in this diagram must be black or white, while the grey squares could still be either:
![](javascript:showlimage("nonogram-alphabet1.png"))
Next, suppose that the letter we're looking at is the leftmost letter in our nonogram, and consider the row clues.
We have to be a little bit careful here: we know that each row clue starts with the clue for the letter, but we don't know which numbers come next:
it could be possible to fit more or fewer of the row's black squares into the first letter.
Looking at the row clues carefully for each letter, we can add some more squares to our squares that we're certain are black or white (if our letter is leftmost):
![](javascript:showlimage("nonogram-alphabet2.png"))
We can now take another look at the columns using this new information, leading to:
![](javascript:showlimage("nonogram-alphabet3.png"))
And another look at the rows then the columns once again leave no grey squares:
![](javascript:showlimage("nonogram-alphabet4.png"))
Overall, this means that given any nonogram built from my alphabet, you can always solve the leftmost
letter. But if you then delete the first letter, you can solve for the second letter (as it's now the
first letter in the shorter nonogram). Then you can solve the third letter, and so on until you've
shown you can solve the full nonogram.
×3 ×7 ×1 ×2(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
⭐ top comment (2025-06-08) ⭐
If you did numbers as well, you could make a meta nonogram, with the completed nonogram having numbers along the top and left, and gridlines. Or it could be a solved nonogram!Boltí
×1 Add a Comment