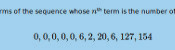Blog
Logic bot, pt. 2
2015-03-15
A few months ago, I set
@mathslogicbot (and @logicbot@mathstodon.xyz and @logicbot.bsky.social) going on the
long task of tweeting all the tautologies (containing 140 characters or less)
in propositional calculus with the symbols \(\neg\) (not), \(\rightarrow\)
(implies), \(\leftrightarrow\) (if and only if), \(\wedge\) (and) and \(\vee\)
(or). My first post on logic bot contains a full
explanation of propositional calculus, formulae and tautologies.
An alternative method
Since writing the original post, I have written an alternative script to
generate all the tautologies.
In this new method, I run through all possible strings of length 1 made
with character in the logical language, then strings of length 2, 3 and so on.
The script then checks if they are valid formulae and, if so, if they are
tautologies.
In the new script, only formulae where the first appearances of variables
are in alphabetical order are considered. This means that duplicate tautologies
are removed. For example, \((b\rightarrow(b\wedge a))\) will now be counted as
it is the same as \((a\rightarrow(a\wedge b))\).
You can view or download this alternative code on
github.
All the terms of the sequence that I have calculated so far can be viewed
here and the tautologies for these terms are
here.
Sequence
One advantage of this method is that it generates the tautologies sorted by
the number of symbols they contain, meaning we can generate the sequence whose
\(n\)th term is the number of tautologies of length \(n\).
The first ten terms of this sequence are
$$0, 0, 0, 0, 2, 2, 12, 6, 57, 88$$
as there are no tautologies of length less than 5; and, for example two
tautologies of length 6 (\((\neg a\vee a)\) and \((a\vee \neg a)\)).
This sequence is listed as
A256120 on OEIS.
Properties
There are a few properties of this sequence that can easily be shown.
Throughout this section I will use \(a_n\) to represent the \(n\)th
term of the sequence.
Firstly, \(a_{n+2}\geq a_n\). This can be explained as follows: let \(A\)
be a tautology of length \(n\). \(\neg\neg A\) will be of length \(n+2\) and
is logically equivalent to \(A\).
Another property is \(a_{n+4}\geq 2a_n\): given a tautology \(A\) of length
\(n\), both \((a\vee A)\) and \((A\vee a)\) will be tautologies of length
\(n+4\). Similar properties could be shown for \(\rightarrow\),
\(\leftrightarrow\) and \(\wedge\).
Given properties like this, one might predict that the sequence will be
increasing (\(a_{n+1}\geq a_n\)). However this is not true as \(a_7\) is 12
and \(a_8\) is only 6. It would be interesting to know at how many points in
the sequence there is a term that is less than the previous one. Given the
properties above it is reasonable to conjecture that this is the only one.
Edit: The sequence has been published on OEIS!
Edit: Added Mastodon and Bluesky links
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
⭐ top comment (2023-02-09) ⭐
Great project! Would be interesting to have a version of this for the sheffer stroke.om
Add a Comment