Blog
Dragon curves
2016-03-30
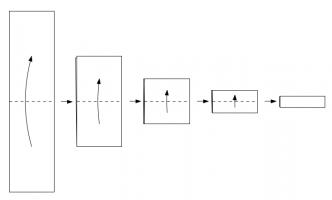
Take a piece of paper. Fold it in half in the same direction many times. Now unfold it. What pattern will the folds make?
![](javascript:showlimage("folding.png"))
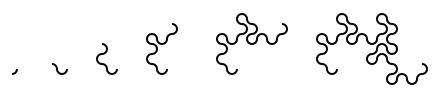
I first found this question in one of Martin Gardner's books. At first, you might that the answer will be simple, but if you look at the shapes made for a few folds, you will see otherwise:
![](javascript:showlimage("young-dragons.png"))
Dragon curves of orders 1 to 6.
The curves formed are called dragon curves as they allegedly look like dragons with smoke rising from their nostrils. I'm not sure I see the resemblance:
![](javascript:showlimage("drawn-dragon.png"))
An order 10 dragon curve.
As you increase the order of the curve (the number of times the paper was folded), the dragon curve squiggles across more of the plane, while never crossing itself. In fact, if the process was continued forever, an order infinity dragon curve would cover the whole plane, never crossing itself.
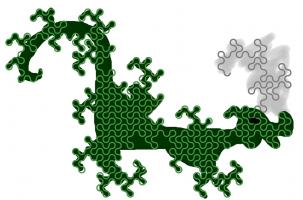
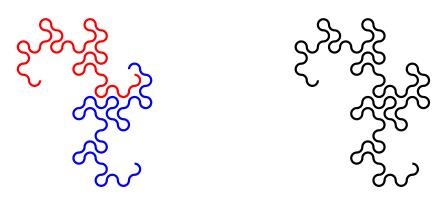
This is not the only way to cover a plane with dragon curves: the curves tessellate.
![](javascript:showlimage("dragon-tile.png"))
When tiled, this picture demonstrates how dragon curves tessellate. For a demonstration, try obtaining infinite lives...
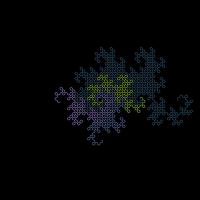
Dragon curves of different orders can also fit together:
![](javascript:showlimage("fd1.png"))
![](javascript:showlimage("fd2.png"))
![](javascript:showlimage("fd3.png"))
Drawing dragon curves
To generate digital dragon curves, first notice that an order \(n\) curve can be made from two order \(n-1\) curves:
![](javascript:showlimage("dragon-recursion.png"))
This can easily be seen to be true if you consider folding paper: If you fold a strip of paper in half once, then \(n-1\) times, each half of the strip will have made an order \(n-1\) dragon curve. But the whole strip has been folded \(n\) times, so is an order \(n\) dragon curve.
Because of this, higher order dragons can be thought of as lots of lower order dragons tiled together. An the infinite dragon curve is actually equivalent to tiling the plane with a infinite number of dragons.
If you would like to create your own dragon curves, you can download the Python code I used to draw them from GitHub. If you are more of a thinker, then you might like to ponder what difference it would make if the folds used to make the dragon were in different directions.
×3 ×3 ×3 ×3 ×3(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment