Blog
World Cup stickers 2018
2018-03-22
Back in 2014, I worked out the cost of filling an official Panini World Cup 2014 sticker book. Today, the 2018 sticker book was relased: compared to four years ago, there are more stickers to collect and the prices have all changed. So how much should we expect it to cost us to fill the album this time round?
How many stickers will I need?
There are 682 stickers to collect. Imagine you have already stuck \(n\) stickers into your album. The probability that the next sticker you buy is new is
$$\frac{682-n}{682}.$$
The probability that the second sticker you buy is the next new sticker is
$$\mathbb{P}(\text{next sticker is not new})\times\mathbb{P}(\text{sticker after next is new})$$
$$=\frac{n}{682}\times\frac{682-n}{682}.$$
Following the same method, we can see that the probability that the \(i\)th sticker you buy is the next new sticker is
$$\left(\frac{n}{682}\right)^{i-1}\times\frac{682-n}{682}.$$
Using this, we can calculate the expected number of stickers you will need to buy until you find a new one:
$$\sum_{i=1}^{\infty}i \left(\frac{682-n}{682}\right) \left(\frac{n}{682}\right)^{i-1} = \frac{682}{682-n}$$
Therefore, to get all 682 stickers, you should expect to buy
$$\sum_{n=0}^{681}\frac{682}{682-n} = 4844 \text{ stickers}.$$
How much will this cost?
You can buy the following [source]:
- Starter pack (an album and 31 stickers) for £3.99
- Sticker packs (5 stickers) for 80p
- Sticker multipacks (30 stickers) for £4.50
First of all you'll need to buy the starter pack, as you need an album to stick everything in. This comes with 31 stickers; we should expect to buy 4813 more stickers after this.
The cheapest way to buy these stickers is to buy them in multipacks for 15p per sticker. This gives a total expected cost of filling the sticker album of £725.94. (Although if your local newsagent doesn't stock the multipacks, buying 80p packs to get these stickers will cost you £774.07.)
What if I order the last 50 stickers?
If you'd like to spend a bit less on the sticker book, Panini lets you order the last 50 stickers to complete your album. This is very helpful as these last 50 stickers are the most expensive.
You can order missing stickers from the Panini website for 22p per sticker's sticker ordering service for the 2018 World Cup doesn't appear to be online yet; but based on other recent collections, it looks like ordered stickers will cost 16p each, with £1 postage per order.
Ordering the last 50 stickers reduces the expected number of other stickers you need to buy to
$$\sum_{n=0}^{631}\frac{682}{682-n} = 1775 \text{ stickers}.$$
This reduces the expected overall cost to £291.03. So I've just saved you £434.91.
What if I order more stickers?
Of course, if you're willing to completely give up on your morals, you could order more than one batch of 50 stickers from Panini. This raises the question: how many should you order to minimise the expected cost.
If you order the last \(a\) stickers, then you should expect to pay:
- £3.99 for the album and first 31 stickers
- £\(\displaystyle0.15\left(\sum_{n=1}^{681-a}\frac{682}{682-n}-31\right)\) for other stickers you need
- £\(\displaystyle \left(0.16a+\left\lceil \frac{a}{50}\right\rceil\right)\) to order the last \(a\) stickers
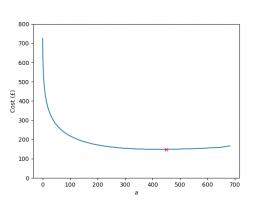
The total expected cost of filling your album for different values of \(a\) is shown in the graph below.
The red cross shows the point at which the album is cheapest: this is when the last 550 stickers are ordered, giving a total expected cost of £120.18. That's another £170.85 I've saved you. You're welcome.
Still, ordering nearly all stickers to minimise the cost doesn't sound like the most fun way to complete the sticker book, so you probably need to order a few less than this to maximise your fun.
What about swaps?
Of course, you can also get the cost of filling the book down by swapping your spare stickers with friends. In 2016, I had a go at simulating filling a sticker book with swapping and came to the possibly obvious conclusion that the more friends you have to swap with, the cheaper filling the book will become.
My best advice for you, therefore, is to get out there right now and start convinding your friends to join you in collecting stickers.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Helpful article!! My head always go into a spine with probability, but does the fact that you would not get a double within a pack affect the overall strategy or cost? My head says this is an another advantage of buying 30 packs over the 5.
RM
Add a Comment



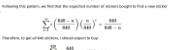

I'm not certain whether they guarantee that there are no duplicates in a pack or just it's very unlikely... Follow up post looking into this coming soon