Puzzles
25 December
It's nearly Christmas and something terrible has happened: there's been a major malfunction in multiple machines in Santa's toy factory, and
not enough presents have been made. Santa has a backup warehouse full of wrapped presents that can be used in the case of severe emergency, but the warehouse is locked.
You need to help Santa work out the code to unlock the warehouse so that he can deliver the presents before Christmas is ruined for everyone.
The information needed to work out the code to the warehouse is known by Santa and his three most trusted elves: Santa is remembering a three-digit number,
and each elf is remembering a one-digit and a three-digit number. If Santa and the elves all agree that the emergency warehouse should be opened, they can work out the code for the door as follows:
- Santa tells his three-digit number to the first elf.
- The first elf subtracts her three-digit number then multiplies by her one-digit number. She tells her result to the second elf.
- The second elf subtracts his three-digit number then multiplies by his one-digit number. He tells his result to the third elf.
- The third elf subtracts their three-digit number then multiplies by their one-digit number. Their result is a five-digit number that is the code to unlock the warehouse.
But this year, there is a complication: the three elves are on a diplomatic mission to Mars to visit Martian Santa and cannot be contacted, so you need to piece together their
numbers from the clues they have left behind:
21
138 is an elf's 3-digit number.
11
The third elf's 1-digit number is not 2.
18
The first elf's 1-digit number is not 6.
1
144 is an elf's 3-digit number.
15
The third elf's 1-digit number is not 7.
23
The HCF of the first and third elves' 1-digit numbers is not 1, 2, or 8.
12
The second elf's 1-digit number is not 2, 8, or 1.
8
The third elf's 1-digit number is not a factor of 575.
17
The first elf's 1-digit number is not 9.
20
The third elf's 1-digit number is not 4.
7
The third elf's 1-digit number is not 1.
4
The third elf's 1-digit number is not 9.
6
990 is a multiple of an elf's 3-digit number.
3
The first elf's 1-digit number is not 7.
22
The HCF of 851 and the third elf's 3-digit number is 1.
14
The second elf's 1-digit number is not 6, 2, or 5.
24
Santa's number is 444.
9
The first elf's 1-digit number is not 5.
5
The second elf's 1-digit number is not 1, 7, or 9.
10
The second elf's 1-digit number is not 4, 9, or 5.
13
One of the digits of the second elf's 3-digit number is 9.
19
The HCF of 256 and the second elf's 3-digit number is 1.
2
The first elf's 1-digit number is not a factor of 202.
16
The first elf's 1-digit number is not 3.
21
138 is an elf's 3-digit number.
11
The third elf's 1-digit number is not 2.
18
The first elf's 1-digit number is not 6.
1
144 is an elf's 3-digit number.
15
The third elf's 1-digit number is not 7.
23
The HCF of the first and third elves' 1-digit numbers is not 1, 2, or 8.
12
The second elf's 1-digit number is not 2, 8, or 1.
8
The third elf's 1-digit number is not a factor of 575.
17
The first elf's 1-digit number is not 9.
20
The third elf's 1-digit number is not 4.
7
The third elf's 1-digit number is not 1.
4
The third elf's 1-digit number is not 9.
6
990 is a multiple of an elf's 3-digit number.
3
The first elf's 1-digit number is not 7.
22
The HCF of 851 and the third elf's 3-digit number is 1.
14
The second elf's 1-digit number is not 6, 2, or 5.
24
Santa's number is 444.
9
The first elf's 1-digit number is not 5.
5
The second elf's 1-digit number is not 1, 7, or 9.
10
The second elf's 1-digit number is not 4, 9, or 5.
13
One of the digits of the second elf's 3-digit number is 9.
19
The HCF of 256 and the second elf's 3-digit number is 1.
2
The first elf's 1-digit number is not a factor of 202.
16
The first elf's 1-digit number is not 3.
You can to open the door here.
24 December
There are 343 three-digit numbers whose digits are all 1, 2, 3, 4, 5, 6, or 7. What is the
mean of all these numbers?
23 December
In a grid of squares, each square is friendly with itself and friendly with every square that is horizontally, vertically, or diagonally adjacent to it (and is not friendly with any other squares).
In a 5×5 grid, it is possible to colour 8 squares so that every square is friendly with at least two coloured squares:
It it not possible to do this by colouring fewer than 8 squares.
What is the fewest number of squares that need to be coloured in a
23×23 grid so that every square is friendly with at least two coloured squares?
22 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number that can be formed using the three digits in the red boxes.
| + | ÷ | = 3 | |||
| – | × | × | |||
| + | – | = 6 | |||
| – | – | – | |||
| × | × | = 16 | |||
| = 1 | = 13 | = 16 |
21 December
Noel wants to write a different non-zero digit in each of the five boxes below so that
the products of the digits of the three-digit numbers reading across and down are the same.
What is the smallest three-digit number that Noel could write in the boxes going across?
20 December
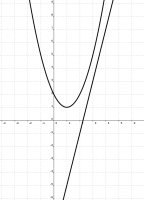
p(x) is a polynomial with integer coefficients such that:
- p(0) > 0;
- if x is a real number, 4x – 9 < p(x) < x2 – 2x + 2.
What is p(23)?
19 December
There are 9 integers below 100 whose digits are all non-zero and add up to 9:
9, 18, 27, 36, 45, 54, 63, 72, and 81.
How many positive integers are there whose digits are all non-zero and add up to 9?
18 December
If k = 21, then 28k ÷ (28 + k) is an integer.
What is the largest integer k such that 28k ÷ (28 + k) is an integer?