Advent calendar 2023
25 December
It's nearly Christmas and something terrible has happened: a machine in Santa's toy factory has malfunctioned, and is unable to finish building all
the presents that Santa needs.
You need to help Santa work out how to fix the broken machine so that he can build the presents and deliver them before Christmas is ruined for everyone.
Inside the broken machine, there were five toy production units (TPUs) installed at sockets labelled A to E. During the malfunction, these TPUs were
so heavily damaged that Santa is unable to identify which TPU they were when trying to fix the machine. The company that supplies TPUs builds 10 different units, numbered from 0 to 9.
You need to work out which of the 10 TPUs needs to be installed in each of the machine's sockets, so that Santa can fix the machine. It may be that two or more of the TPUs are the same.
21
C is not 2.
11
E is not 0.
18
One or more of the TPUs is 1
1
C is 1, 8, or 0.
15
C is 4, 4, or 4.
23
The clues on day 9 and day 23 are false.
12
Exactly 2 of the TPUs is/are even.
8
Exactly two of the TPUs are 2.
17
A is 2 and B is 2.
20
Exactly 4 of the TPUs is/are even.
7
D is 9, 8, or 7.
4
E is 2 or 6.
6
E is 2, 3, or 3.
3
A is 5.
22
E is not 7.
14
C is not 3, 9, or 9.
24
Strictly less than 10 clues are true.
9
The clues on days that are factors of 600 are false.
5
D is 3, 7, or 8.
10
C is 5.
13
E is not 8+1.
19
E is not 5 or 4
2
C is 6, 8, or 1.
16
A is 2 and B is 1.
You can attempt to fix the machine
here.
Show answer
Hide answer
The only way that the clue on day 23 doesn't lead to a contradiction is if clue 23 is false and clue 9 is true. Clue 9 being true means that clues
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, and 24 are all false. So far, we know:
| True clues: | 9 |
| False clues: | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 20, 23, 24 |
| Unknown: | 7, 11, 13, 14, 16, 17, 18, 19, 21, 22 |
Clue 24 being false means that at least 10 of the clues are true, so at most 1 of the unknown clues is false. Clues 16 and 17 contradict each other, so one of these is false and every other
currently unknown clue is true:
| True clues: | 7, 9, 11, 13, 14, 18, 19, 21, 22 |
| False clues: | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 20, 23, 24 |
| Unknown: | 16, 17 |
From the clues we know to be true or false plus knowing that one of 16 and 17 is true, we now know that
A is 2,
B is 1 or 2,
C is 7,
D is 9,
and E is 1 or 8.
We also know that one or more TPU is 1, there are not exactly 2 or exactly 4 even TPUs
and there are not exactly two TPUs that are 2. The last of these clues tell us that B cannot be 2,
and so is 1 and:
| True clues: | 7, 9, 11, 13, 14, 16, 18, 19, 21, 22 |
| False clues: | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 17, 20, 23, 24 |
In order to avoid having exactly 2 even TPUs, E must not be 8, and so
we conclude that A is 2, B is 1, C is 7, D is 9, and E is 1.
24 December
When written in binary, the number 235 is 11101011. This binary representation starts and
ends with 1 and does not contain two 0s in a row.
What is the smallest three-digit number whose binary representation starts and
ends with 1 and does not contain two 0s in a row?
Show answer
Hide answer
- 100 in binary is 1100100;
- 101 in binary is 1100101;
- 102 in binary is 1100110;
- 103 in binary is 1100111;
- 104 in binary is 1101000;
- 105 in binary is 1101001;
- 106 in binary is 1101010;
- 107 in binary is 1101011;
23 December
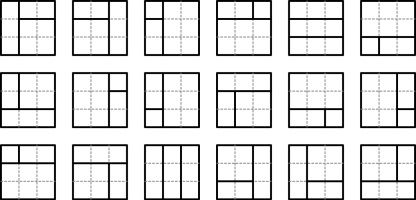
There are 18 ways to split a 3 by 3 square into 3 rectangles whose sides all have integer length:
How many ways are there to split a 10 by 10 square into 3 rectangles whose sides all have integer length?
Show answer
Hide answer
The square is split into 3 rectangles by drawing two lines on the rectangle. There are two cases: the lines can both go
in the same direction; or the lines go in perpendicular directions, with one going all the way across the square and one going from an edge of the square to the other line.
For an \(n\) by \(n\) square, there are:
- \((n-1)(n-2)/2\) ways to pick two dividing lines that are both vertical;
- \((n-1)(n-2)/2\) ways to pick two dividing lines that are both horizontal;
- \(2(n-1)(n-1)\) ways to pick two dividing lines where one is vertical and goes all the way across the square, and the other is horizontal.
- \(2(n-1)(n-1)\) ways to pick two dividing lines where one is horizontal and goes all the way across the square, and the other is vertical;
In total this makes \((n-1)(5n-6)\) ways to split the square. (10–1)×(5×10-6) is 396.
22 December
There are 4 ways to pick three vertices of a regular quadrilateral so that they form a right-angled triangle:
In another regular polygon with \(n\) sides, there are 14620 ways to pick three vertices so that they form a right-angled triangle. What is \(n\)?
Show answer
Hide answer
The vertices of any regular polygon lie on a circle, and so the three vertices we pick must lie on this circle. The triangle will be right-angled
if one of the edges of the triangle is a diameter of the circle.
If the regular polygon has \(n=2k\) sides, then there are \(k\) ways to pick two points that make a diameter, and \(2k-2\) ways to pick the third point to make the triangle, and so there are
a total of \(k(2k-2)=n(n-2)/2\) right-angled triangles. This means that we need to solve \(n(n-2)/2=14620\). The solution is \(n=172\), and so our polygon has 172 sides.
21 December
There are 6 two-digit numbers whose digits are all 1, 2, or 3 and whose second digit onwards
are all less than or equal to the previous digit:
How many 20-digit numbers are there whose digits are all 1, 2, or 3 and whose second digit onwards
are all less than or equal to the previous digit?
Show answer & extension
Hide answer & extension
We can look at how many \(n\)-digit number there are for small values of \(n\) and look for a pattern:
- 1-digit numbers: there are 3.
- 2-digit numbers: there are 6.
- 3-digit numbers: there are 10.
- 4-digit numbers: there are 15.
These are the triangle numbers, and there are 231 20-digit numbers.
Extension
Why is the pattern the triangle numbers?
20 December
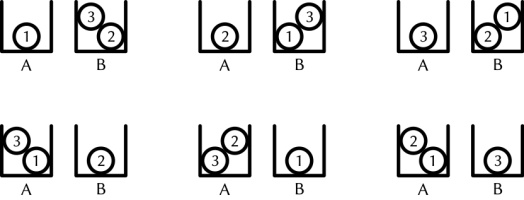
There are 6 different ways that three balls labelled 1 to 3 can be put into two boxes labelled
A and B so that no box is empty:
How many ways can five balls labelled 1 to 5 be put into four boxes labelled A to D so that
no box is empty?
Show answer
Hide answer
One method for putting the five balls into the four boxes is:
pick one of the balls (there are 5 ways to do this), then put the other four balls into boxes with one in each box (there are 4! ways to do this), then
put the picked ball into a box (there are 4 ways to do this). This method gives exactly two ways of obtaining each possible arrangement, so the number of
ways is \(5\times4!\times4\div2\) or 240.
19 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | – | | = 7 |
| × | | × | | × | |
| + | | – | | = 0 |
| ÷ | | ÷ | | ÷ | |
| + | | – | | = 2 |
=
4 | | =
35 | | =
18 | |
Show answer
Hide answer
| 8 | + | 5 | – | 6 | = 7 |
| × | | × | | × | |
| 2 | + | 7 | – | 9 | = 0 |
| ÷ | | ÷ | | ÷ | |
| 4 | + | 1 | – | 3 | = 2 |
=
4 | | =
35 | | =
18 | |
The product of the numbers in the red boxes is 504.
18 December
Some numbers can be written as the product of two or more consecutive integers, for example:
$$6=2\times3$$
$$840=4\times5\times6\times7$$
What is the smallest three-digit number that can be written as the product of two or more consecutive integers?
17 December
If you expand \((a+b+c)^2\), you get \(a^2+b^2+c^2+2ab+2ac+2bc\).
This has 6 terms.
How many terms does the expansion of \((a+b+c+d+e+f)^5\) have?
16 December
Some numbers can be written as the sum of two or more consecutive positive integers, for example:
$$7=3+4$$
$$18=5+6+7$$
Some numbers (for example 4) cannot be written as the sum of two or more consecutive positive integers.
What is the smallest three-digit number that cannot be written as the sum of two or more consecutive positive integers?
Show answer & extension
Hide answer & extension
Every number except the powers of 2 can be written as the sum of two or more consecutive positive integers. The smallest
three-digit power of 2 is 128.
Extension
Why can every number that isn't a power of 2 be written as the sum of two or more consecutive positive integers?
15 December
The arithmetic mean of a set of \(n\) numbers is computed by adding up all the numbers, then
dividing the result by \(n\).
The geometric mean of a set of \(n\) numbers is computed by multiplying all the numbers together, then
taking the \(n\)th root of the result.
The arithmetic mean of the digits of the number 132 is \(\tfrac13(1+3+2)=2\).
The geometric mean of the digits of the number 139 is \(\sqrt[3]{1\times3\times9}\)=3.
What is the smallest three-digit number whose first digit is 4 and for which the arithmetic and geometric means of its digits are both non-zero integers?
Show answer & extension
Hide answer & extension
The only three digit number whose first digits is 4 and for which the arithmetic and geometric means of its digits are both non-zero integers is 444.
Extension
How many three digit numbers are there for which the arithmetic and geometric means of its digits are both non-zero integers?
How many four digit numbers are there for which the arithmetic and geometric means of its digits are both non-zero integers?
14 December
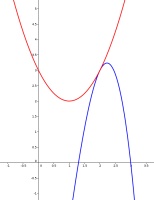
The function \(f(x)=ax+b\) (where \(a\) and \(b\) are real constants) satisfies
$$-x^3+2x^2+6x-9\leqslant f(x)\leqslant x^2-2x+3$$
whenever \(0\leqslant x\leqslant3\). What is \(f(200)\)?
Show answer
Hide answer
How to get started with this puzzle is easiest to see if we plot the two curves:
We see that the two curves meet at the point (2,3). The only way that the straight line \(f\) can be between the two curves is if it is a tangent to both curves.
By differentiation of another way of finding tangents, you can show that \(a=2\) and \(b=1\). Therefore \(f(200)\) is 399.
13 December
Today's number is given in this crossnumber. No number in the completed grid starts with 0.
|
|
| Across |
| 1 | Today's number. | (3) |
| 4 | A multiple of 5 times the sum of the digits of 2D. | (3) |
| 5 | Greater than two times 3D. | (3) |
|
| Down |
| 1 | The sum of 5A and 3D. | (3) |
| 2 | Nine times the sum of the digits of 4A. | (3) |
| 3 | Greater than 2D. | (3) |
|
Show answer
Hide answer
2D is a multiple of 9, and so its digits add up to a multiple of 9. This means that 4A is a multiple of 9, and its digits add up to a multiple of 9 too.
The digits of 4A can add up to at most 27 (if it's 999) and so must add add up to 9, 18, or 27. These would make 2D equal to 81, 162, or 243 respectively. 2D cannot be 81 (as it's a three-digit number);
it also can't be 243, as this would mean 4A was 999, leading to a clash in the centre square. Therefore the sum of the digits of 4A is 18 and 2D is 162:
The sum of the digits of 4A is 18, so 4A is 369, 468, 567, 666, 765, 864, or 963. Of these, only 765 is a multiple of 5, and so 4A must be 765:
3D is greater than 2D, so the first digit of 3D is at least 2. If the first digit of 3D was 3 or higher, then 5A would be greater than 700, meaning 1D would be greater than 1000 and not a three-digit number.
Therefore:
The last digits of 3D and 5A are the same, and so the last digit of 1D (and the first digit of 5A) must be even. 5A is greater than 500, and so it's first digit must be 6 or 8;
it cannot be 8 as this would make 1D greater than 100. And so:
This only leaves one option for the last two digits to make 1D's clue correct:
Today's number is 812.
12 December
What is the smallest value of \(n\) such that
$$\frac{500!\times499!\times498!\times\dots\times1!}{n!}$$
is a square number?
Show answer
Hide answer
Consider the first two terms in the product:
$$
500!\times499!
=500\times499!\times499!$$
$$= 500\times(499!)^2.$$
Doing similar steps with each pair of terms in the product, we see that:
$$
500!\times499!\times498!\times\dots\times1!
=
500\times498\times\dots\times2\times(499!\times497!\times\dots\times1!)^2
$$
$$
=
(2\times250)\times(2\times249)\times\dots\times(2\times1)\times(499!\times497!\times\dots\times1!)^2
$$
$$
=
2^{250}\times250!\times(499!\times497!\times\dots\times1!)^2
$$
If we divide this by \(250!\), we are left with a square number, and so \(n\) is 250
11 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | + | | = 15 |
| + | | + | | ÷ | |
| + | | – | | = 10 |
| + | | – | | × | |
| ÷ | | × | | = 3 |
=
16 | | =
1 | | =
30 | |
Show answer
Hide answer
| 3 | + | 7 | + | 5 | = 15 |
| + | | + | | ÷ | |
| 9 | + | 2 | – | 1 | = 10 |
| + | | – | | × | |
| 4 | ÷ | 8 | × | 6 | = 3 |
=
16 | | =
1 | | =
30 | |
The product of the numbers in the red boxes is 120.
10 December
How many integers are there between 100 and 1000 whose digits add up to an even number?
Show answer
Hide answer
Between 100 and 109 (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number.
Between 110 and 119 (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number...
In general, between \(10n\) and \(10n+9\) (inclusive), there are 5 integers whose digits add up to an even number, and 5 whose digits add up to an odd number.
The integers from 100 to 999 (inclusive) can be split into 45 sets of integers from \(10n\) to \(10n+9\) (and the digits of 1000 don't add to an even number), so there are
450 integers between 100 and 1000 whose digits add up to an even number.
9 December
The diagram below shows a rectangle. Two of its sides have been coloured blue. A red line has been drawn from two of its vertices to the midpoint of a side.
The total length of the blue lines is 50cm. The total length of the red lines is also 50cm. What is the area of the rectangle (in cm2)?
Show answer
Hide answer
Let \(a\) be the height of the rectangle. As the total of the blue lines is 50, the width of the rectangle is \(50-a\).
As the total of the red lines is 50, each red line segment is 25.
Using Pythagoras's theorem in one of the right-angled triangles, we see that:
$$a^2 + \left(\frac{50-a}{2}\right)^2 = 25^2$$
$$4a^2 + (50-a)^2 = 50^2$$
$$4a^2 + 50^2 - 100a + a^2 = 50^2$$
$$a(5a - 100) = 0$$
\(a\) is not zero, and so \(a=20\). This means that the area of the rectangle is 20×30=600.
8 December
Noel writes the numbers 1 to 17 in a row. Underneath, he writes the same list without the first and last numbers, then continues this until he writes a row containing just one number:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| | | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | | |
| etc. |
What is the sum of all the numbers that Noel has written?
7 December
There are 8 sets (including the empty set) that contain numbers from 1 to 4 that don't include any consecutive integers:
\(\{\}\), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{4\}\), \(\{1,3\}\), \(\{1,4\}\), \(\{2, 4\}\)
How many sets (including the empty set) are there that contain numbers from 1 to 14 that don't include any consecutive integers?
6 December
There are 5 ways to tile a 4×2 rectangle with 2×1 pieces:
How many ways are there to tile a 12×2 rectangle with 2×1 pieces?
Show answer
Hide answer
Let \(a_n\) be the number of ways to tile a \(n\times2\) rectangle.
It is easy to check that \(a_1=1\) (ie there is 1 way to tile a 1×2 rectangle) and \(a_2=2\) (ie there are 2 ways to tile a 2×2 rectangle).
For an \(n\times2\) rectangle, from the left the tiling either starts with a vertical tile, or a pair of horizontal tiles.
If it starts with a vertical tile, then there are \(a_{n-1}\) ways to tile the remaining \((n-1)\times2\) rectangle.
If it starts with a pair of horizontal tile2, then there are \(a_{n-2}\) ways to tile the remaining \((n-2)\times2\) rectangle.
Therefore, \(a_n=a_{n-1}+a_{n-2}\).
(And so the number of ways to tile a \(n\times2\) rectangle is the \((n+1)\)th Fibonacci number.)
Therefore, the number of ways to tile a 12×2 rectangle is 233.
5 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | + | | = 15 |
| + | | – | | + | |
| + | | + | | = 15 |
| + | | × | | ÷ | |
| + | | + | | = 15 |
=
15 | | =
15 | | =
15 | |
Show answer
Hide answer
| 2 | + | 6 | + | 7 | = 15 |
| + | | – | | + | |
| 4 | + | 3 | + | 8 | = 15 |
| + | | × | | ÷ | |
| 9 | + | 5 | + | 1 | = 15 |
=
15 | | =
15 | | =
15 | |
The product of the numbers in the red boxes is 378.
4 December
If \(n\) is 1, 2, 4, or 6 then \((n!-3)/(n-3)\) is an integer. The largest of these numbers is 6.
What is the largest possible value of \(n\) for which \((n!-123)/(n-123)\) is an integer?
Show answer
Hide answer
We can split this fraction into:
$$\frac{n!}{n-123}-\frac{123}{n-123}$$
As long as \(n\) is larger than 123, \(n-123\) is positive and less than \(n\). This means that \(n!/(n-123)\) is an integer, as \(n-123\) will be one of the numbers multiplied together in \(n!\).
(\((124!-123)/(124-123)\) is an integer, so the answer is at least 124 and \(n!/(2-123)\) is an integer when \(n\) is the answer.)
We now need to answer the simpler question: What is the largest value of \(n\) for which \(123/(n-123)\) is an integer? This will be when \(n-123\) is equal to 123, and so \(n\) is 246.
3 December
190 is the smallest multiple of 10 whose digits add up to 10.
What is the smallest multiple of 15 whose digits add up to 15?
2 December
Holly adds up the first six even numbers, then adds on half of the next even number. Her total is 49.
Next, Holly adds up the first \(n\) even numbers then adds on half of the next even number. This time, her total is 465124. What is \(n\)?
Show answer & extension
Hide answer & extension
If we add up the first \(n\) even numbers then add on half of the next even number, we get \((n+1)^2\). This means that Holly added up the first \(\sqrt{465124}-1\) or 681 even numbers.
Extension
Can you show why adding up the first \(n\) even numbers and half of the next even number gives \((n+1)^2\)?
1 December
Each interior angle of a regular triangle is 60°.
Each interior angle of a different regular polygon is 178°. How many sides does this polygon have?
Show answer
Hide answer
The exterior angles of any polygon add up to 360°.
The interior angles of our polygon are 178°, and so the exterior angles are 2°. There must be 180 sides (and so also 180 angles) on the polygon, as 180×2=360.