Puzzles
1 December
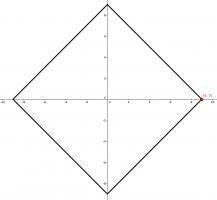
One of the vertices of a rectangle is at the point \((9, 0)\). The \(x\)-axis and \(y\)-axis are both lines of symmetry of the rectangle.
What is the area of the rectangle?
Show answer
Hide answer
The only way this is possible is if the rectangle is this square:
The area of this square is 162.
Placing plates
Two players take turns placing identical plates on a square table. The player who is first to be unable to place a plate loses. Which player wins?
Show answer & extension
Hide answer & extension
The first player can always win by first placing a plate on the exact centre of the table. Then the first player can copy what the second player does, but rotated 180°, and hence can always place a plate if the second player could.
Extension
What if the two players play on a regular hexagonal table? Or a regular octagonal table? Or a regular pentagonal table? Or a regular \(n\)-gonal table?
![](javascript:showlimage("ad2022-1ans.png"))