Puzzles
6 December
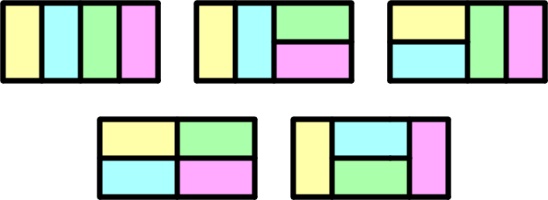
There are 5 ways to tile a 4×2 rectangle with 2×1 pieces:
How many ways are there to tile a 12×2 rectangle with 2×1 pieces?
Show answer
Hide answer
Let \(a_n\) be the number of ways to tile a \(n\times2\) rectangle.
It is easy to check that \(a_1=1\) (ie there is 1 way to tile a 1×2 rectangle) and \(a_2=2\) (ie there are 2 ways to tile a 2×2 rectangle).
For an \(n\times2\) rectangle, from the left the tiling either starts with a vertical tile, or a pair of horizontal tiles.
If it starts with a vertical tile, then there are \(a_{n-1}\) ways to tile the remaining \((n-1)\times2\) rectangle.
If it starts with a pair of horizontal tile2, then there are \(a_{n-2}\) ways to tile the remaining \((n-2)\times2\) rectangle.
Therefore, \(a_n=a_{n-1}+a_{n-2}\).
(And so the number of ways to tile a \(n\times2\) rectangle is the \((n+1)\)th Fibonacci number.)
Therefore, the number of ways to tile a 12×2 rectangle is 233.
7 December
There are 15 dominos that can be made using the numbers 0 to 4 (inclusive):
The sum of all the numbers on all these dominos is 60.
Today's number is the sum of all the numbers on all the dominos that can be made using the numbers 5 to 10 (inclusive).
Show answer
Hide answer
Each number will appear 7 times: one time paired with the numbers six numbers 5 to 10, plus an extra appearance on the tile containing the same number twice.
The total of all the numbers is therefore 7×(5+6+...+10)=7×45=315.
4 December
There are 5 ways to tile a 3×2 rectangle with 2×2 squares and 2×1 dominos.
Today's number is the number of ways to tile a 9×2 rectangle with 2×2 squares and 2×1 dominos.
Show answer
Hide answer
Let \(a_n\) be the number of ways to tile an \(n\times2\) rectangle.
There is one way to tile a 1×2 rectangle; and there are three ways to tile a 2×2 rectangle. Therefore \(a_1=1\) and \(a_2=3\).
In a \(n\times2\) rectangle, the rightmost column will either contain a vertical 2×1 domino, two horizontal 2×1 dominoes, or a 2×2 square.
Therefore \(a_n=a_{n-1}+2a_{n-2}\).
Using this, we find that there are 341 ways to tile a 9×2 rectangle.