Puzzles
23 December
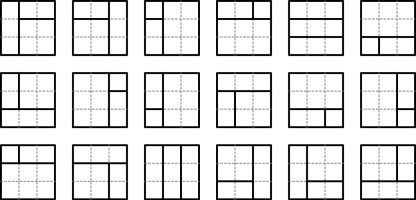
There are 18 ways to split a 3 by 3 square into 3 rectangles whose sides all have integer length:
How many ways are there to split a 10 by 10 square into 3 rectangles whose sides all have integer length?
Show answer
Hide answer
The square is split into 3 rectangles by drawing two lines on the rectangle. There are two cases: the lines can both go
in the same direction; or the lines go in perpendicular directions, with one going all the way across the square and one going from an edge of the square to the other line.
For an \(n\) by \(n\) square, there are:
- \((n-1)(n-2)/2\) ways to pick two dividing lines that are both vertical;
- \((n-1)(n-2)/2\) ways to pick two dividing lines that are both horizontal;
- \(2(n-1)(n-1)\) ways to pick two dividing lines where one is vertical and goes all the way across the square, and the other is horizontal.
- \(2(n-1)(n-1)\) ways to pick two dividing lines where one is horizontal and goes all the way across the square, and the other is vertical;
In total this makes \((n-1)(5n-6)\) ways to split the square. (10–1)×(5×10-6) is 396.
9 December
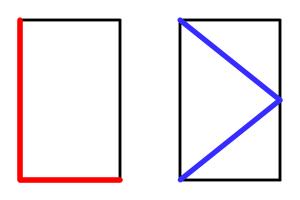
The diagram below shows a rectangle. Two of its sides have been coloured blue. A red line has been drawn from two of its vertices to the midpoint of a side.
The total length of the blue lines is 50cm. The total length of the red lines is also 50cm. What is the area of the rectangle (in cm2)?
Show answer
Hide answer
Let \(a\) be the height of the rectangle. As the total of the blue lines is 50, the width of the rectangle is \(50-a\).
As the total of the red lines is 50, each red line segment is 25.
Using Pythagoras's theorem in one of the right-angled triangles, we see that:
$$a^2 + \left(\frac{50-a}{2}\right)^2 = 25^2$$
$$4a^2 + (50-a)^2 = 50^2$$
$$4a^2 + 50^2 - 100a + a^2 = 50^2$$
$$a(5a - 100) = 0$$
\(a\) is not zero, and so \(a=20\). This means that the area of the rectangle is 20×30=600.
1 December
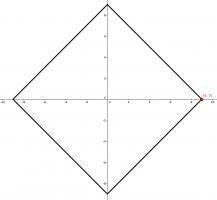
One of the vertices of a rectangle is at the point \((9, 0)\). The \(x\)-axis and \(y\)-axis are both lines of symmetry of the rectangle.
What is the area of the rectangle?
Show answer
Hide answer
The only way this is possible is if the rectangle is this square:
The area of this square is 162.
Equal lengths
The picture below shows two copies of the same rectangle with red and blue lines. The blue line visits the midpoint of the opposite side. The lengths shown in red and blue are of equal length.
What is the ratio of the sides of the rectangle?
Show answer
Hide answer
Let \(a\) be the height of the rectangle and \(b\) be the width.
The length of the red line is \(a+b\). The length of the blue line is \(2\sqrt{a^2+\frac{b^2}4}\). These are equal so:
\begin{align}
a+b&=2\sqrt{a^2+\frac{b^2}4}\\
(a+b)^2&=4\left(a^2+\frac{b^2}{4}\right)\\
a^2+2ab+b^2&=4a^2+b^2\\
0&=3a^2-2ab\\
0&=3a-2b\\
2b&=3a
\end{align}
Therefore the ratio of the sides is 2:3.
1 December
What is area of the largest area rectangle which will fit in a circle of radius 10?
Show answer
Hide answer
The largest rectangle will be a square. 20 (double the radius) will be the length of its diagonal.
By Pythagoras' Theorem, the sides of the square are \(10\sqrt{2}\). Therefore the area of the square is 200.