Puzzles
7 December
What is the obtuse angle in degrees between the minute and hour hands of a clock at 08:22?
Show answer
Hide answer
Every hour, the hour hand moves 360÷12 = 30°.
Every minute, the hour hand moves 30÷60 = ½° and the minute hand moves 360÷60 = 6°.
At 8:22, the hour hand will be 8×30+22×½ = 251° from the top of the clock
and the minute hand will be 22×6 = 132° from the top of the clock. The angle between the hands will
be 251-132 = 119°.
1 December
Each interior angle of a regular triangle is 60°.
Each interior angle of a different regular polygon is 178°. How many sides does this polygon have?
Show answer
Hide answer
The exterior angles of any polygon add up to 360°.
The interior angles of our polygon are 178°, and so the exterior angles are 2°. There must be 180 sides (and so also 180 angles) on the polygon, as 180×2=360.
Is it equilateral?
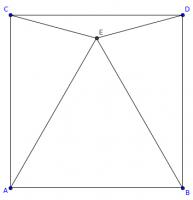
In the diagram below, \(ABDC\) is a square. Angles \(ACE\) and \(BDE\) are both 75°.
Is triangle \(ABE\) equilateral? Why/why not?
Show answer
Hide answer
The triangle is equilateral.
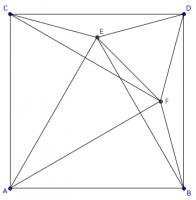
To see why, add a copy of point \(E\) rotated by 90°. This is labelled \(F\) on the diagram below.
Angles \(BDE\) and \(CDF\) are both 75°. Therefore angles \(CDE\) and \(BDF\) are both 15°. This means that angle \(FDE\) is 60°.
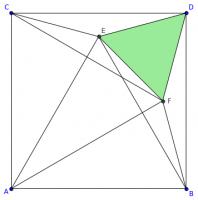
Line \(AD\) is a line of symmetry of the diagram, so angles \(DFE\) and \(DEF\) are equal and both 60°. Therefore, triangle DEF is equilateral. This triangle is show in green in the diagram below.
Lines \(EF\), \(DF\) and \(BF\) are all equal length, so triangles \(BFE\) and \(BFD\) are isosceles.
Angles \(BDF\) and \(FBD\) are both 15°. Angles \(FBE\) and \(FEB\) are equal, and the angles in triangle \(BED\) add to 180°: this means that angle \(FBE\) is 15°.
Angles \(FBE\) and \(FBD\) are both 15°, and so angle \(EBD\) is 30°. Angles \(EBD\) and \(ABE\) add to 90°, and so angle \(ABE\) is 60°.
By symmetry, angle \(BAE\) is also 60°. Angle \(BEA\) must therefore also be 60°, so triangle \(ABE\) is equilateral.
17 December
The number of degrees in one internal angle of a regular polygon with 360 sides.
Ticking clock
Is there a time of day when the hands of an analogue clock (one with a second hand that moves every second instead of moving continuously) will all be 120° apart?
Show answer & extension
Hide answer & extension
The second hand will always be pointing at one of the 60 graduations. If the minute and hour hand are 120° away from the second hand they must also be pointing at one of the graduations. The minute hand will only be pointing at a graduation at zero seconds past the minute, so the second hand must be pointing at 0. Therefore the hand are either pointing at: hour: 4, minute: 8, second: 0; or hour: 8, minute: 4, second: 0. Neither of these are real times, so it is not possible
Extension
If the second hand moves continuously instead of moving every second, will there be a time when the hands of the clock are all 120° apart?
Dodexagon
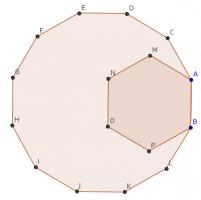
In the diagram, B, A, C, D, E, F, G, H, I, J, K and L are the vertices of a regular dodecagon and B, A, M, N, O and P are the vertices of a regular hexagon.
Show that A, M and E lie on a straight line.
Show answer & extension
Hide answer & extension
The interior angle of a regular hexagon is 120°. The interior angle of a regular dodecagon is 150°. Therefore angle CAM is 30°.
Now, consider the quadrilateral ACDE. This quadrilateral is symmetric (as the dodecagon is regular) so the angles CAE and DEA are equal. Hence:
$$360 = CAE+DEA+ACD+CDE\\
= 2CAE + 2\times 150\\
2CAE = 60\\
CAE=30
$$
The angles CAM and CAE are equal, so A, M and E lie on a straight line.
Extension
The vertices \(P_1\), \(P_2\), ..., \(P_n\) make up a regular \(n\)-gon and \(Q_1\), \(Q_2\), ..., \(Q_m\) make up a regular \(m\)-gon, with \(P_1=Q_1\) and \(P_2=Q_2\).
The vertices \(P_2\), \(Q_3\) and \(P_5\) lie on a straight line. What is the relationship between \(m\) and \(n\)?
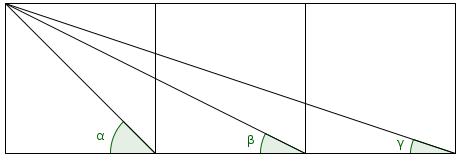
Three squares
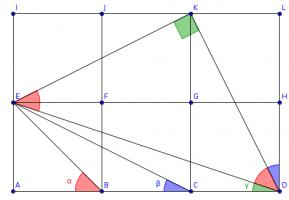
The diagram shows three squares with diagonals drawn on and three angles labelled.
What is the value of \(\alpha+\beta+\gamma\)?
Show answer & extension
Hide answer & extension
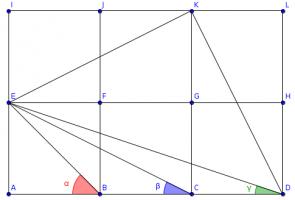
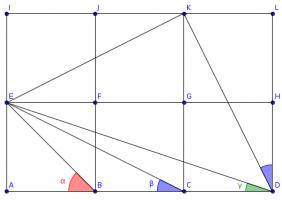
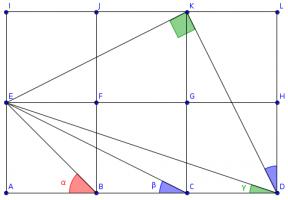
Draw three more squares and add these lines (I have coloured the angles to make equal angles clearer):
Triangles \(ACE\), \(LDK\) and \(IKE\) are congruent, so angle \(KDL\) is equal to \(\beta\).
The congruence of these triangles tells us that angles \(DKL\) and \(EKI\) add up to a right angle, so angle \(EKD\) is also a right angle.
The congruence of the triangles also tells us that \(KD\) and \(KE\) are the same length and so angle \(EDK\) is the angle in an isosceles right-angled triangle. \(\alpha\) is also the angle in an isosceles right-angled triangle, so these two angles are equal.
Therefore \(\alpha+\beta+\gamma=90^\circ\).
Extension
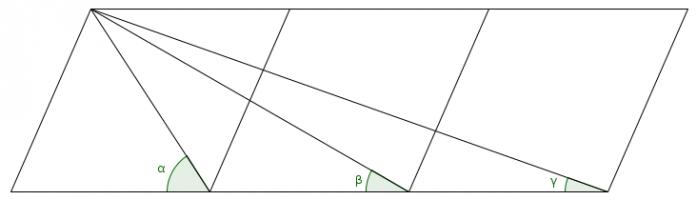
The diagram shows three rhombuses with diagonals drawn on and three angles labelled.
What is the value of \(\alpha+\beta+\gamma\)?