Puzzles
8 December
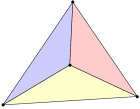
It is possible to arrange 4 points on a plane and draw non-intersecting lines
between them to form 3 non-overlapping triangles:
It is not possible to make more than 3 triangles with 4 points.
What is the maximum number of non-overlapping triangles that can be made by arranging 290 points on a plane
and drawing non-intersecting lines between them?
Show answer
Hide answer
By adding a point inside a triangle, you can turn one triangle into three triangles. By adding a point outside all the current triangles, you can add either
one or two more triangles. As we are after the maximum number of triangles, we will choose to add two triangles for each point we add.
Four points make 3 triangles. Adding 286 more points will add 572 more triangles, giving a total of 575.
22 December
There are 4 ways to pick three vertices of a regular quadrilateral so that they form a right-angled triangle:
In another regular polygon with \(n\) sides, there are 14620 ways to pick three vertices so that they form a right-angled triangle. What is \(n\)?
Show answer
Hide answer
The vertices of any regular polygon lie on a circle, and so the three vertices we pick must lie on this circle. The triangle will be right-angled
if one of the edges of the triangle is a diameter of the circle.
If the regular polygon has \(n=2k\) sides, then there are \(k\) ways to pick two points that make a diameter, and \(2k-2\) ways to pick the third point to make the triangle, and so there are
a total of \(k(2k-2)=n(n-2)/2\) right-angled triangles. This means that we need to solve \(n(n-2)/2=14620\). The solution is \(n=172\), and so our polygon has 172 sides.
20 December
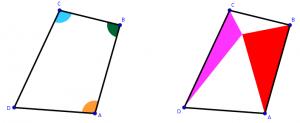
The diagram to the right shows (two copies of) quadrilateral ABCD.
The sum of the angles ABC and BCD (green and blue in quadrilateral on the left) is 180°.
The sum of the angles ABC and DAB (green and orange in quadrilateral on the left) is also 180°.
In the diagram on the right, a point inside the quadrilateral has been used to draw two triangles.
The area of the quadrilateral is 850. What is the smallest that the total area of the two triangles
could be?
Show answer
Hide answer
The angles adding up to 180° implies that AD and BC are parallel and AB and DC are parellel, and so the quadrilateral is a parallelogram.
The total area of the triangles will always be half the parallelogram, or 425.
7 December
What is the area of the largest triangle that fits inside a regular hexagon with area 952?
Show answer
Hide answer
The vertices of this triangle will be every other vertex of the hexagon: and other triangle can be made larger by moving one of its vertices closer to a vertex of the hexagon.
The area of this triangle is 476.
20 December
What is the area of the largest area triangle that has one side of length 32 and one side of length 19?
Show answer
Hide answer
The triangle will be largest when the two sides meet at a right angle. The area of this triangle is ½×32×19=304.
13 December
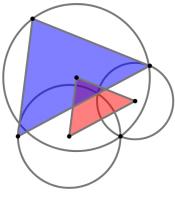
The diagram to the left shows three circles and two triangles. The three circles all meet at one point.
The vertices of the smaller red triangle are at the centres of the circles. The lines connecting the
vertices of the larger blue triangle to the point where all three circles meet are diameters of the
three circles.
The area of the smaller red triangle is 226. What is the area of the larger blue triangle?
Show answer
Hide answer
The two triangles are similar, and the sides of the blue triangle are twice the length of the red triangle. Therefore the area of the blue triangle
is 4 times the area of the red triangle. 226×4=904.
7 December
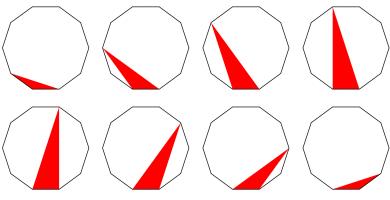
The picture below shows eight regular decagons. In each decagon, a red triangle has been drawn with vertices at three of the vertices of the decagon.
The area of each decagon is 240. What is the total area of all the red triangles?
Show answer
Hide answer
By rotating the triangles, they can be made to exactly cover the decagon.
The total area of all the triangles is therefore 240.
5 December
How many different isosceles triangles are there whose perimeter is 50 units, and whose area is an integer number of square-units?
(Two triangles that are rotations, reflections and translations of each other are counted as the same triangle. Triangles with an area of 0 should not be counted.)
Show answer
Hide answer
The largest possible isosceles triangles with a perimeter of 50 units is the equilateral triangle with sides of length 50/3. The area of this triangle is 120.28 square-units.
By continuously adjusting the width of the base of the isosceles triangle, triangles with every area between 0 and 120.28 can be created. The animation below shows this.
Triangles with areas of each integer from 1 to 120 can therefore be created. Each area can be made twice: once with a tall and thin triangle, and once with a short and wide triangle.
This means that there are 240 different triangles with a perimeter of 50 units and an integer area.
![](javascript:showlimage("advent2024-8dec.png"))
![](javascript:showlimage("advent2023-22dec.png"))
![](javascript:showlimage("advent2022-20corrected.png"))
![](javascript:showlimage("advent2021-circles.png"))
![](javascript:showlimage("advent2021-decagons.png"))
![](javascript:showlimage("advent2021-dodec-ans.png"))
![](javascript:showlimage("advent2021-isosceles.gif"))