Puzzles
6 December
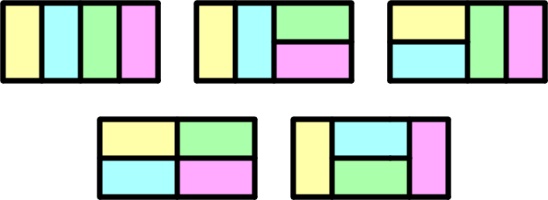
There are 5 ways to tile a 4×2 rectangle with 2×1 pieces:
How many ways are there to tile a 12×2 rectangle with 2×1 pieces?
Show answer
Hide answer
Let \(a_n\) be the number of ways to tile a \(n\times2\) rectangle.
It is easy to check that \(a_1=1\) (ie there is 1 way to tile a 1×2 rectangle) and \(a_2=2\) (ie there are 2 ways to tile a 2×2 rectangle).
For an \(n\times2\) rectangle, from the left the tiling either starts with a vertical tile, or a pair of horizontal tiles.
If it starts with a vertical tile, then there are \(a_{n-1}\) ways to tile the remaining \((n-1)\times2\) rectangle.
If it starts with a pair of horizontal tile2, then there are \(a_{n-2}\) ways to tile the remaining \((n-2)\times2\) rectangle.
Therefore, \(a_n=a_{n-1}+a_{n-2}\).
(And so the number of ways to tile a \(n\times2\) rectangle is the \((n+1)\)th Fibonacci number.)
Therefore, the number of ways to tile a 12×2 rectangle is 233.
4 December
There are 5 ways to tile a 3×2 rectangle with 2×2 squares and 2×1 dominos.
Today's number is the number of ways to tile a 9×2 rectangle with 2×2 squares and 2×1 dominos.
Show answer
Hide answer
Let \(a_n\) be the number of ways to tile an \(n\times2\) rectangle.
There is one way to tile a 1×2 rectangle; and there are three ways to tile a 2×2 rectangle. Therefore \(a_1=1\) and \(a_2=3\).
In a \(n\times2\) rectangle, the rightmost column will either contain a vertical 2×1 domino, two horizontal 2×1 dominoes, or a 2×2 square.
Therefore \(a_n=a_{n-1}+2a_{n-2}\).
Using this, we find that there are 341 ways to tile a 9×2 rectangle.