Puzzles
17 December
If you expand \((a+b+c)^2\), you get \(a^2+b^2+c^2+2ab+2ac+2bc\).
This has 6 terms.
How many terms does the expansion of \((a+b+c+d+e+f)^5\) have?
14 December
The function \(f(x)=ax+b\) (where \(a\) and \(b\) are real constants) satisfies
$$-x^3+2x^2+6x-9\leqslant f(x)\leqslant x^2-2x+3$$
whenever \(0\leqslant x\leqslant3\). What is \(f(200)\)?
Show answer
Hide answer
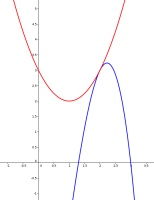
How to get started with this puzzle is easiest to see if we plot the two curves:
We see that the two curves meet at the point (2,3). The only way that the straight line \(f\) can be between the two curves is if it is a tangent to both curves.
By differentiation of another way of finding tangents, you can show that \(a=2\) and \(b=1\). Therefore \(f(200)\) is 399.
18 December
The expansion of \((x+y+z)^3\) is
$$x^3 + y^3 + z^3 + 3x^2y + 3x^2z + 3xy^2 + 3y^2z + 3xz^2 + 3yz^2 + 6xyz.$$
This has 10 terms.
Today's number is the number of terms in the expansion of \((x+y+z)^{26}\).
Show answer
Hide answer
In each term, the powers of \(x\), \(y\) and \(z\) must add to 26: the terms will be of the form \(x^iy^jz^{26-i-j}\).
If \(i=0\), there are 27 choices for \(j\) (0 to 26).
If \(i=1\), there are 26 choices for \(j\) (0 to 25).
If \(i=2\), there are 25 choices for \(j\) (0 to 24).
...
If \(i=26\), there is 1 choice for \(j\) (0).
Therefore the total number of terms is 27+26+25+...+1 = 378.
10 December
For all values of \(x\), the function \(f(x)=ax+b\) satisfies
$$8x-8-x^2\leqslant f(x)\leqslant x^2.$$
What is \(f(65)\)?
Edit: The left-hand quadratic originally said \(8-8x-x^2\). This was a typo and has now been corrected.
Show answer
Hide answer
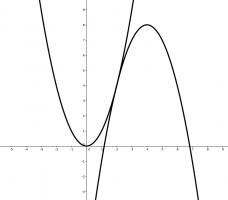
If we plot the two quadratics, we see that they meet at \(x=2\) where they both have gradient 4.
The line \(f(x)\) must therefore pass through the point \((2,4)\) and have gradient 4, so its equation is \(f(x)=4x-4\).
This means that \(f(65)\) is 256.
7 December
The sum of the coefficients in the expansion of \((x+1)^5\) is 32. Today's number is the sum of the coefficients in the expansion of \((2x+1)^5\).
Show answer
Hide answer
The sum of the coefficients can be found by substituting \(x=1\) into the expression. Hence the sum of the coefficients in the expansion of \((2x+1)^5\) is
\(3^5\), or 243.
18 December
There are 6 terms in the expansion of \((x+y+z)^2\):
$$(x+y+z)^2=x^2+y^2+z^2+2xy+2yz+2xz$$
Today's number is number of terms in the expansion of \((x+y+z)^{16}\).
10 December
The equation \(x^2+1512x+414720=0\) has two integer solutions.
Today's number is the number of (positive or negative) integers \(b\) such that \(x^2+bx+414720=0\) has two integer solutions.
Show answer
Hide answer
If the equation has two integer solutions, then it can be written as \((x+\alpha)(x+\beta)\), where \(\alpha\) and \(\beta\) are integers.
Expanding this and setting it equal to \(x^2+bx+414720=0\), we find that \(b=\alpha+\beta\) and \(414720=\alpha\beta\).
414720 has 55 different pairs of factors. Each of these pairs leads to two values of \(b\) (a positive and a negative value). Therefore there are 110 values of \(b\) that give the equation two integer solutions.
Powerful quadratics
Find all real solutions to
$$(x^2-7x+11)^{(x^2-11x+30)}=1.$$
Show answer
Hide answer
If \(x^2-7x+11=1\) or \(x^2-11x+30=0\), then this is one. The solutions to these are \(x=2,5,\) and \(6\).
It could also be one if \(x^2-7x+11=-1\) and \(x^2-11x+30\) is even. This happens when \(x=3\) or \(4\).
Therefore all the solutions to this are \(x=2,3,4,5\) or \(6\).
![](javascript:showlimage("advent2023sol-14dec.png"))
![](javascript:showlimage("advent2019quads.png"))
