Advent calendar 2020
Advent 2020 logic puzzle
It's nearly Christmas and something terrible has happened: you've just landed in a town in the Arctic circle with a massive bag of letters for Santa, but
you've lost to instructions for how to get to Santa's house near the north pole.
You need to work out where he lives and deliver the letters to him before Christmas is ruined for everyone.
Due to magnetic compasses being hard to use near the north pole, you brought with you a special Advent compass. This compass has nine numbered directions.
Santa has given the residents of the town clues about a sequence of directions that will lead to his house;
but in order to keep his location secret from present thieves,
he gave each resident two clues: one clue is true, and one clue is false.
Here are the clues:
9
"The 4th digit is
4."
"The 8th digit is
4."
4
"The 3rd digit is
1."
"The 4th digit is
7."
10
"The 11th digit is a factor of
888."
"The 11th digit is a factor of 88."
13
"The 3rd digit is
1."
"The 4th digit is
6."
23
"The 10th digit is
4."
"The 10th digit is
3."
1
"The last digit is
1,
9 or
5."
"The last digit is
1."
5
"The 3rd digit is
1."
"The 4th digit is
3."
16
"The 5th digit is
3."
"The 6th digit is
3."
11
"The sequence's length is
2+
1+
6."
"The sequence's length is
2×
1×
6."
12
"The 6th to 8th digits are
3,
3,
4."
"The 7th to 9th digits are
3,
3,
4."
2
"The 7th digit is
4."
"The 8th digit is
4."
21
"The 5th digit is
3."
"The 9th digit is
9."
22
"The 9th digit is
9."
"The 10th digit is
4."
17
"The 3rd digit is
1."
"The 4th digit is
9."
15
"The 2nd* digit is
7."
"The 1st digit is
8."
14
"The 1st digit is
7."
"The 2nd digit is
7."
7
"The last digit is not
5."
"The 4th digit is
5."
3
"The 11th digit is a factor of 10."
"The 11th digit is a factor of
321."
6
"The sequence's length is
1+
9+
2."
"The sequence's length is
1×
9×
2."
20
"The 5th digit is
3."
"The 5th digit is
4."
19
"
5 does not appear."
"
5 appears exactly once."
24
"The 3rd digit is
1."
"The 4th digit is
8."
18
"The 1st digit is
3,
7 or
8."
"The sequence's length is prime."
8
"The 3rd digit is
1."
"The 4th digit is
2."
You can view the map
here.
Show answer
Hide answer
Santa's house could be found by following the directions 3,7,1,1,4,3,3,4,9,3,3,9.
24 December
There are six ways to put two tokens in a 3 by 3 grid so that the diagonal from the top left to the bottom right is a line of symmetry:
Today's number is the number of ways of placing two tokens in a 29 by 29 grid so that the diagonal from the top left to the bottom right is a line of symmetry.
Show answer
Hide answer
Either both pieces must be on the diagonal, or one pieces is in the lower right half and the other is in the reflected position in the upper right half.
There are \(\left(\begin{array}{c}29\\2\end{array}\right)=406\) ways to pick two squares on the diagonal. There are 406 squares below the diagonal.
Therefore there are 406+406 = 812 ways to arrange the pieces.
23 December
198 is the smallest number that is equal to 11 times the sum of its digits.
Today's number is the smallest number that is equal to 48 times the sum of its digits.
Show answer
Hide answer
We're looking for a number \(n\) such that the digits of \(n\times48\) add up to \(n\). If we try numbers in order, we find that 9 works, so today's number is 432.
22 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number you can make with the digits in the red boxes.
| + | | + | | = 18 |
| + | | + | | + | |
| ÷ | | - | | = 1/2 |
| + | | + | | + | |
| + | | ÷ | | = 3/2 |
=
24 | | =
8 | | =
13 | |
Show answer
Hide answer
| 9 | + | 5 | + | 4 | = 18 |
| + | | + | | + | |
| 7 | ÷ | 2 | - | 3 | = 1/2 |
| + | | + | | + | |
| 8 | + | 1 | ÷ | 6 | = 3/2 |
=
24 | | =
8 | | =
13 | |
The largest number you can make with the digits in the red boxes is 984.
21 December
There are 3 ways to order the numbers 1 to 3 so that no number immediately follows the number one less that itself:
Today's number is the number of ways to order the numbers 1 to 6 so that no number immediately follows the number one less that itself.
Show answer
Hide answer
To make sequences of 4 numbers, we can insert 4s into three different places in the length 3 sequences given to obtain:
- 4, 3, 2, 1
- 3, 2, 4, 1
- 3, 2, 1, 4
- 4, 1, 3, 2
- 1, 4, 3, 2
- 1, 3, 2, 4
- 4, 2, 1, 3
- 2, 4, 1, 3
- 2, 1, 4, 3
There are some possibilities missing: those containing \(i, 4, i+1\). These can be found by taking the sequences of length 2, picking a number \(i\), adding 1 to every number larger than \(i\), then replacing \(i\) with \(i\ 4\ i+1\).
- 2, 1 → 3, 1 → 3, 1, 4, 2
- 2, 1 → 2, 1 → 2, 4, 3, 1
This gives a total of 3×3+2×1=11 sequences for 4 numbers.
To make sequences with 5 numbers, we can insert 5s into four different places in the length 4 sequences. This gives 4×11=44 sequences.
The missing sequences can then be found by taking the sequences of length 3, then doing the same process as above:
- 3, 2, 1 → 3, 2, 1 → 3, 5, 4, 2, 1
- 3, 2, 1 → 4, 2, 1 → 4, 2, 5, 3, 1
- 3, 2, 1 → 4, 3, 1 → 4, 3, 1, 5, 2
- 1, 3, 2 → 1, 4, 3 → 1, 5, 2, 4, 3
- 1, 3, 2 → 1, 3, 2 → 1, 3, 5, 4, 2
- 1, 3, 2 → 1, 4, 2 → 1, 4, 2, 5, 3
- 2, 1, 3 → 2, 1, 4 → 2, 5, 3, 1, 4
- 2, 1, 3 → 3, 1, 4 → 3, 1, 5, 2, 4
- 2, 1, 3 → 2, 1, 3 → 2, 1, 3, 5, 4
There are 3×3=9 of these, giving 44+9 = 53 total sequences of length 5.
To make sequences with 6 numbers, we can insert 6s into five different places in the length 5 sequences. This gives 5×53=265 sequences.
We can also make sequence by picking a number to replace in the length 4 sequences. This gives 4×11=44 more sequences.
Therefore there are 265+44 = 309 sequences in total.
20 December
18 can be written as the sum of 3 consecutive (strictly) positive integers: 5 + 6 + 7.
18 can also be written as the sum of 4 consecutive (strictly) positive integers: 3 + 4 + 5 + 6.
18 is in fact the smallest number that can be written as the sum of both 3 and 4 consecutive (strictly) positive integers.
Today's number is the smallest number that can be written as the sum of both 12 and 13 consecutive (strictly) positive integers.
Show answer
Hide answer
The sum of 13 consecutive integers is 13 times the middle number, so today's number is a multiple of 13.
The sum of 12 consecutive integers is 6 times the sum of the two middle numbers, so today's number is also a multiple of 6.
Therefore today's number is a multiple of 78.
78 and 156 do not work (the numbers would not all be strictly positive), so today's number is 234.
19 December
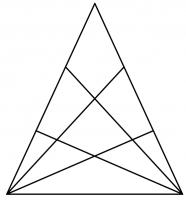
The diagram to the right shows a triangle. Two of the sides of the triangle have been split into three pieces, with lines drawn from the opposite vertex. In total, the diagram now contains 27 triangles of any size.
Another triangle has two of its sides split into eight pieces, with lines drawn from the opposite vertex. How many triangles (of any size) would this create?
Show answer
Hide answer
Each triangle must include one of the two corners at the base of the largest triangle (or both those corners).
To make triangles including the bottom left corner of the large triangle, we must pick two lines coming out of that corner, and one line coming out of the bottom right corner that is not the base of the triangle.
There are 9 lines coming out of the corners, so the total number of triangles is \(\left(\begin{array}{c}9\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=288\).
We now need to count the triangles that include the bottom right corner of the large triangle, but do not include both corners (as we've already counted thoses).
There are \(\left(\begin{array}{c}8\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=224\) ways to pick lines to make these triangles.
In total, this makes 512 triangles.
18 December
The expansion of \((x+y+z)^3\) is
$$x^3 + y^3 + z^3 + 3x^2y + 3x^2z + 3xy^2 + 3y^2z + 3xz^2 + 3yz^2 + 6xyz.$$
This has 10 terms.
Today's number is the number of terms in the expansion of \((x+y+z)^{26}\).
Show answer
Hide answer
In each term, the powers of \(x\), \(y\) and \(z\) must add to 26: the terms will be of the form \(x^iy^jz^{26-i-j}\).
If \(i=0\), there are 27 choices for \(j\) (0 to 26).
If \(i=1\), there are 26 choices for \(j\) (0 to 25).
If \(i=2\), there are 25 choices for \(j\) (0 to 24).
...
If \(i=26\), there is 1 choice for \(j\) (0).
Therefore the total number of terms is 27+26+25+...+1 = 378.
17 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums and product are correct.
Today's number is the product of the numbers in the red boxes.
| + | | + | | = 16 |
| + | | + | | + | |
| + | | + | | = 8 |
| + | | + | | + | |
| × | | × | | = 288 |
=
11 | | =
14 | | =
20 | |
Show answer
Hide answer
| 6 | + | 3 | + | 7 | = 16 |
| + | | + | | + | |
| 1 | + | 2 | + | 5 | = 8 |
| + | | + | | + | |
| 4 | × | 9 | × | 8 | = 288 |
=
11 | | =
14 | | =
20 | |
The product of the numbers in the red boxes is 189.
16 December
Solve the crossnumber to find today's number. No number starts with 0.
|
|
| Across |
| 1 | 3 more than a multiple of 110. | (3) |
| 4 | Today's number. | (3) |
| 5 | 30 more than a multiple of 101. | (3) |
| Down |
| 1 | 37 times the sum of 1A's digits. | (3) |
| 2 | 3 times a factor of 5A. | (3) |
| 3 | 3 less than a multiple of 112. | (3) |
|
15 December
When talking to someone about this Advent calendar, you told them that the combination of XMAS and MATHS is GREAT.
They were American, so asked you if the combination of XMAS and MATH is great; you said SURE. You asked them their name; they said SAM.
Each of the letters E, X, M, A, T, H, S, R, U, and G stands for a different digit 0 to 9. The following sums are correct:
Today's number is SAM. To help you get started, the letter T represents 4.
14 December
The numbers 33, 404 and 311 contain duplicate digits. The numbers 120, 15 and 312 do not.
How many numbers between 10 and 999 (inclusive) contain no duplicate digits?
Show answer
Hide answer
There are 81 two-digit numbers with no duplicate digits: there are 9 choices of tens digit (1 to 9), and for each of these there are 9 remaining choices
for the units digit (0 to 9 but not the number already used).
There are 648 three-digit numbers with no duplicate digits: there are 9 choices of hundreds digit (1 to 9), and for each of these there are 9 remaining choices
for the tens digit (0 to 9 but not the number already used) and 8 choices for the units digit (0 to 9 but neight number already used).
648+81 = 729.
13 December
There are 6 ways to split the sequence of the numbers 1 to 5 into three shorter sequences:
- 1 and 2 and 3, 4, 5
- 1 and 2, 3 and 4, 5
- 1 and 2, 3, 4 and 5
- 1, 2 and 3 and 4, 5
- 1, 2 and 3, 4 and 5
- 1, 2, 3 and 4 and 5
Today's number is the number of ways to split the sequence of the numbers 1 to 10 into five shorter sequences.
Show answer
Hide answer
There are 9 gaps between the numbers 1 to 10. We need to pick 5 of these gaps to split the sequence. There are \(\left(\begin{array}{c}9\\5\end{array}\right)\) ways to do this:
this is 126.
12 December
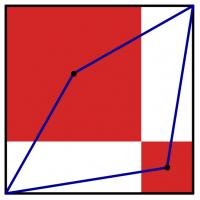
The diagram to the left shows a large black square. Inside this square, two red squares have been drawn.
(The sides of the red squares are parallel to the sides of the black square; each red square shares a vertex with the black square; and the two red squares share a vertex.)
A blue quadrilateral has then been drawn with vertices at two corners of the black square and the centres of the red squares.
The area of the blue quadrilateral is 167. What is the area of the black square?
Show answer
Hide answer
No matter the exact size of each square, the blue quadrilateral will always fill half the square, so the area of the square is 334.
11 December
Noel has a large pile of cards. Half of them are red, the other half are black. Noel splits the cards into two piles: pile A and pile B.
Two thirds of the cards in pile A are red. Noel then moves 108 red cards from pile A to pile B. After this move, two thirds of the cards in pile B are red.
How many cards did Noel start with?
Note: There was a mistake in the original version of today's puzzle. The number 21 has been replaced with 108.
Show answer
Hide answer
Let's say there were originally \(t\) cards of each colour, and \(2a\) red cards and \(a\) black cards in pile A.
After the move, there were \(t-2a+108\) red cards and \(t-a\) black cards in pile B. Two thirds of the card in pile B are red, so:
$$t-2a+108=2(t-a)$$
$$t=108$$
Therefore there were 108×2=216 cards.
Interestingly, it appears that this answer is independent of \(a\): any number of cards could be put in each pile and this situation would still work. However, only one situation could have happened
unless you allow there to at some points have been a negative number of cards in each pile.
10 December
Today's number is the smallest multiple of 24 whose digits add up to 24.
Show answer
Hide answer
There are one three-digit even numbers whose digits add to 24: 798, 888 and 996. Of these, only 888 is a multiple of 24.
9 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | | × | | = 54 |
| × | | + | | ÷ | |
| - | | ÷ | | = 1 |
| ÷ | | - | | × | |
| + | | - | | = 6 |
=
18 | | =
6 | | =
18 | |
Show answer
Hide answer
| 4 | + | 5 | × | 6 | = 54 |
| × | | + | | ÷ | |
| 9 | - | 8 | ÷ | 1 | = 1 |
| ÷ | | - | | × | |
| 2 | + | 7 | - | 3 | = 6 |
=
18 | | =
6 | | =
18 | |
The product of the numbers in the red boxes is 144.
8 December
The residents of Octingham have 8 fingers. Instead of counting in base ten, they count in base eight: the digits of their numbers represent ones, eights, sixty-fours, two-hundred-and-fifty-sixes, etc
instead of ones, tens, hundreds, thousands, etc.
For example, a residents of Octingham would say 12, 22 and 52 instead of our usual numbers 10, 18 and 42.
Today's number is what a resident of Octingham would call 11 squared (where the 11 is also written using the Octingham number system).
Show answer
Hide answer
The Octingham resident's 11 is equal to our number 9. 9 squared is 81. 81 in base eight is 121.
Interestingly, this is the same answer as "just" doing 11 squred in base ten.
7 December
There are 15 dominos that can be made using the numbers 0 to 4 (inclusive):
The sum of all the numbers on all these dominos is 60.
Today's number is the sum of all the numbers on all the dominos that can be made using the numbers 5 to 10 (inclusive).
Show answer
Hide answer
Each number will appear 7 times: one time paired with the numbers six numbers 5 to 10, plus an extra appearance on the tile containing the same number twice.
The total of all the numbers is therefore 7×(5+6+...+10)=7×45=315.
6 December
There are 12 ways of placing 2 tokens on a 2×4 grid so that no two tokens are next to each other horizonally, vertically or diagonally:
Today's number is the number of ways of placing 5 tokens on a 2×10 grid so that no two tokens are next to each other horizonally, vertically or diagonally.
Show answer
Hide answer
First, consider placing 5 tiles in a 1×9 grid. There is only one way to do this:
To get the number of ways of placing 5 tiles in a 1×10 grid, imagine adding an extra blank square to either the start or end of the grid or between two of the counters.
There are 6 places this tile could be inserted leading to 6 arrangements of 5 tiles in a 1×10 grid.
For 5 tiles in a 2×10 grid, you can first pick the columns the tiles go in (as a tile being in a column means nothing can be placed the columns either side, the number of ways to pick
columns is the same and the number of wats to arrange 5 tokens in a 1×10 grid). For each of these column choices, there are two locations for each tile (top or bottom).
This leads to a total number of arrangements of 6×25=192. 5 DecemberCarol rolled a large handful of six-sided dice. The total of all the numbers Carol got was 521. After some calculating, Carol worked out that the probability that of her total being 521
was the same as the probability that her total being 200. How many dice did Carol roll? Show answerHide answerThe totals that are equally likely add up to 7 times the number of dice.
This can be seen by using the fact that the opposite sides of a dice add up to 7: for each way of making a given total with \(n\) dice, there is a way of making \(7n\) minus that total
by looking at the dice from below. Therefore \(T\) and \(7n-T\) are equally likely. (This also holds true (but is harder to explain) if you rearrange the faces of the dice so that the opposite
faces no longer add to 7.)
Therefore today's number is \((521+200)/7\), which is 103. 4 DecemberToday's number is a three digit number which is equal to the sum of the cubes of its digits. One less than today's number also has this property. Show answerHide answerIf the final digit of the number is 0, then some carrying takes place when 1 is subtracted. Otherwise, no carrying happens.
If no carrying happens, call the three digits of today's number \(A\), \(B\), and \(C\). We know that \(A^3+B^3+C^3\) is one more than \(A^3 + B^3 + (C-1)^3\).
This implies that \(C^3=(C-1)^3+1\), which is only possible if \(C\) is 1.
Therefore either the final digit of today's number is 0 or the final digt of one less that today's number is 0. In both cases, we need to find a number
with the desired property whose final digit is 0: we are looking for digit \(A\) and \(B\) such that \(A^3+B^3\) is a multiple of 10.
Looking at all the cube numbers, there are a few combinations that add up to multiple of 10:
$$0^3+0^3=0$$
$$1^3+9^3=730$$
$$2^3+8^3=520$$
$$3^3+7^3=370$$
$$4^3+6^3=280$$
$$5^3+5^3=250$$
The only one of these that has the required property is 370. By checking 369 and finding it doesn't have the property, we see that the two numbers must be
370 and 371. 3 DecemberPut the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number you can make with the digits in the red boxes.
| ÷ | | - | | = 3 |
| + | | + | | ÷ | |
| ÷ | | × | | = 1 |
| × | | - | | + | |
| - | | × | | = 20 |
=
91 | | =
6 | | =
8 | |
Show answerHide answer
| 9 | ÷ | 1 | - | 6 | = 3 |
| + | | + | | ÷ | |
| 4 | ÷ | 8 | × | 2 | = 1 |
| × | | - | | + | |
| 7 | - | 3 | × | 5 | = 20 |
=
91 | | =
6 | | =
8 | |
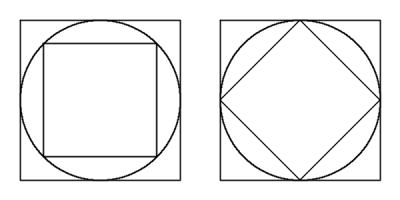
The largest number you can make with the digits in the red boxes is 321. 2 DecemberCarol draws a square with area 62. She then draws the smallest possible circle that this square is contained inside.
Next, she draws the smallest possible square that her circle is contained inside. What is the area of her second square? Show answerHide answerBy drawing an appropriate diagram, it can be seen that the small square has half the area of the large square.
Therefore the area of the large square is 124. 1 DecemberIt is possible to write 325 different numbers using the digits 1, 2, 3, 4, and 5 at most once each (and using no other digits).
How many of these numbers are odd? Show answerHide answerThere are 3 one-digit numbers using these digits (1, 3 and 5).
To make two-digit odd numbers, there are 3 choices for the units digit, and 4 remaining choices for the tens digit.
To make three-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, and 3 remaining choices for the hundreds digit.
To make four-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, 3 remaining choices for the hundreds digit, and 2 remaining choices for the thousands digit.
To make five-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, 3 remaining choices for the hundreds digit, 2 remaining choices for the thousands digit and 1 remaining choice for the ten-thousands digit.
In total, this gives 3 + 3×4× + 3×4×3 + 3×4×3×2 + 3×4×3×2×1 = 195 odd numbers. |