Puzzles
15 December
The number 2268 is equal to the product of a square number (whose last digit is not 0) and the same square number with its digits reversed:
36×63.
What is the smallest three-digit number that is equal to the product of a square number (whose last digit is not 0) and the same square number with its digits reversed?
Show answer
Hide answer
The only three-digit number that is equal to the product of a square number and the same square number with its digits reversed is 16×61 = 976.
23 December
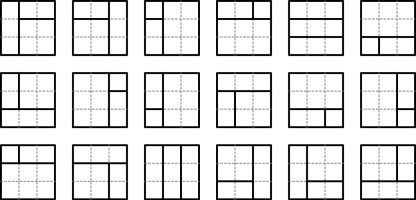
There are 18 ways to split a 3 by 3 square into 3 rectangles whose sides all have integer length:
How many ways are there to split a 10 by 10 square into 3 rectangles whose sides all have integer length?
Show answer
Hide answer
The square is split into 3 rectangles by drawing two lines on the rectangle. There are two cases: the lines can both go
in the same direction; or the lines go in perpendicular directions, with one going all the way across the square and one going from an edge of the square to the other line.
For an \(n\) by \(n\) square, there are:
- \((n-1)(n-2)/2\) ways to pick two dividing lines that are both vertical;
- \((n-1)(n-2)/2\) ways to pick two dividing lines that are both horizontal;
- \(2(n-1)(n-1)\) ways to pick two dividing lines where one is vertical and goes all the way across the square, and the other is horizontal.
- \(2(n-1)(n-1)\) ways to pick two dividing lines where one is horizontal and goes all the way across the square, and the other is vertical;
In total this makes \((n-1)(5n-6)\) ways to split the square. (10–1)×(5×10-6) is 396.
2 December
Carol draws a square with area 62. She then draws the smallest possible circle that this square is contained inside.
Next, she draws the smallest possible square that her circle is contained inside. What is the area of her second square?
Show answer
Hide answer
By drawing an appropriate diagram, it can be seen that the small square has half the area of the large square.
Therefore the area of the large square is 124.
19 December
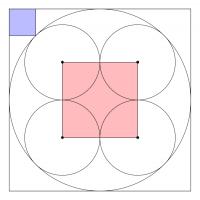
The diagram below shows three squares and five circles.
The four smaller circles are all the same size, and the red square's vertices are the centres of these circles.
The area of the blue square is 14 units. What is the area of the red square?
Show answer
Hide answer
The diagonal of the blue square is \(\sqrt{28}\). The radius \(R\) of the large circle satisfies \(R^2+R^2=(R+\sqrt{28})^2\).
Solving this, we find that \(R=\frac{\sqrt{28}}{\sqrt2-1}=\sqrt{28}(\sqrt2+1)\).
The radius \(r\) of the small circles satisfies \(r+r\sqrt2=R\), and so \(r=\frac{\sqrt{28}(\sqrt2+1)}{\sqrt2+1}=\sqrt{28}\).
The area of the square is \(4r^2=4\left(\sqrt{28}\right)^2=4\times28\). This is 112.
Is it equilateral?
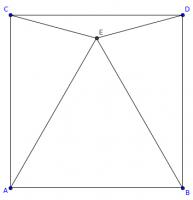
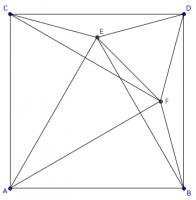
In the diagram below, \(ABDC\) is a square. Angles \(ACE\) and \(BDE\) are both 75°.
Is triangle \(ABE\) equilateral? Why/why not?
Show answer
Hide answer
The triangle is equilateral.
To see why, add a copy of point \(E\) rotated by 90°. This is labelled \(F\) on the diagram below.
Angles \(BDE\) and \(CDF\) are both 75°. Therefore angles \(CDE\) and \(BDF\) are both 15°. This means that angle \(FDE\) is 60°.
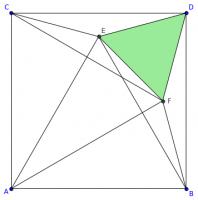
Line \(AD\) is a line of symmetry of the diagram, so angles \(DFE\) and \(DEF\) are equal and both 60°. Therefore, triangle DEF is equilateral. This triangle is show in green in the diagram below.
Lines \(EF\), \(DF\) and \(BF\) are all equal length, so triangles \(BFE\) and \(BFD\) are isosceles.
Angles \(BDF\) and \(FBD\) are both 15°. Angles \(FBE\) and \(FEB\) are equal, and the angles in triangle \(BED\) add to 180°: this means that angle \(FBE\) is 15°.
Angles \(FBE\) and \(FBD\) are both 15°, and so angle \(EBD\) is 30°. Angles \(EBD\) and \(ABE\) add to 90°, and so angle \(ABE\) is 60°.
By symmetry, angle \(BAE\) is also 60°. Angle \(BEA\) must therefore also be 60°, so triangle \(ABE\) is equilateral.
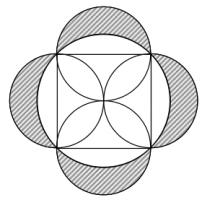
Squared circle
Each side of a square has a circle drawn on it as diameter. The square is also inscribed in a fifth circle as shown.
Find the ratio of the total area of the shaded crescents to the area
of the square.
Show answer
Hide answer
Let the radius of the small circles be \(r\). The are of half of one of these circles is \(\frac{1}{2}\pi r^2\).
The side of the square is \(2r\) and so the area of the square is \(4r^2\). Therefore the area of the whole shape is \((4+2\pi)r^2\).
By Pythagoras' Theorem, the radius of the large circle is \(r\sqrt{2}\). Therefore the area of the circle is \(2\pi r^2\). This means that the shaded area is \((4+2\pi)r^2 - 2\pi r^2\) or \(4r^2\).
This is the same as the area of the square, so the ratio is 1:1.