Puzzles
Cutting corners
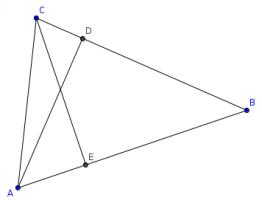
The diagram below shows a triangle \(ABC\). The line \(CE\) is perpendicular to \(AB\) and the line \(AD\) is perpedicular to \(BC\).
The side \(AC\) is 6.5cm long and the lines \(CE\) and \(AD\) are 5.6cm and 6.0cm respectively.
How long are the other two sides of the triangle?
Show answer
Hide answer
Let \(A\), \(B\) and \(C\) represent the angles at points \(A\), \(B\) and \(C\). Looking at triangle \(ACE\) gives:
$$\sin A=\frac{5.6}{6.5}$$
And triangle \(ACD\) gives:
$$\sin C=\frac{6.0}{6.5}$$
Using Pythagoras' Theorem to find the missing sides in these triangles also gives:
$$\cos A=\frac{3.3}{6.5}$$
$$\cos C=\frac{2.5}{6.5}$$
We can use these to find \(\sin B\):
$$\begin{array}{rl}
\sin B&=\sin(\pi-A-C)\\
&=\sin(A+B)\\
&=\sin A\cos C + \cos A\sin C\\
&=\frac{5.6}{6.5}\frac{2.5}{6.5}+\frac{6.0}{6.5}\frac{3.3}{6.5}\\
&=\frac{33.8}{6.5^2}
\end{array}$$
Now the missing sides can be found using the sine rule:
$$\begin{array}{rl}
CB&=\frac{CA\sin A}{\sin B}\\
&=\frac{6.5\times\frac{5.6}{6.5}}{\frac{33.8}{6.5^2}}\\
&=\frac{6.5^2\times5.6}{33.8}\\
&=7\text{cm}
\end{array}$$
$$\begin{array}{rl}
AB&=\frac{CA\sin C}{\sin B}\\
&=\frac{6.5\times\frac{6}{6.5}}{\frac{33.8}{6.5^2}}\\
&=\frac{6.5^2\times6}{33.8}\\
&=7.5\text{cm}
\end{array}$$
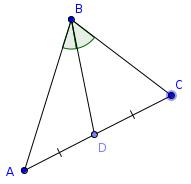
Equal side and angle
In the diagram shown, the lengths \(AD = CD\) and the angles \(ABD=CBD\).
Prove that the lengths \(AB=BC\).
Show answer
Hide answer
By the sine rule in BCD:
$$\frac{CD}{\sin(CBD)}=\frac{BD}{\sin(BCD)}$$
By the sine rule in BAD:
$$\frac{AD}{\sin(ABD)}=\frac{BD}{\sin(BAD)}$$
\(ABD=CBD\) and \(AD=CD\), so:
$$\sin(BAD)=\frac{BD\sin(ABD)}{AD}\\
=\frac{BD\sin(CBD)}{CD}\\
=\sin(BCD)$$
Using the sine rule in ABC:
$$\frac{AB}{\sin(BCD)}=\frac{BC}{\sin(BAD)}$$
The two sines are equal and so:
$$AB=BC$$
Arctan
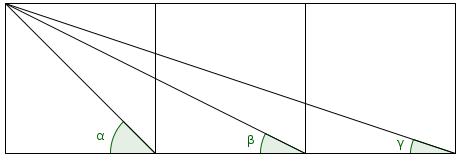
Prove that \(\arctan(1)+\arctan(2)+\arctan(3)=\pi\).
Show answer & extension
Hide answer & extension
Let \(\alpha=\arctan(1)\), \(\beta=\arctan(2)\) and \(\gamma=\arctan(3)\), then draw the angles as follows:
Extension
Can you find any other integers \(a\), \(b\) and \(c\) such that:
$$\arctan(a)+\arctan(b)+\arctan(c)=\pi$$
Sine
A sine curve can be created with five people by giving the following instructions to the five people:
A. Stand on the spot.
B. Walk around A in a circle, holding this string to keep you the same distance away.
C. Stay in line with B, staying on this line.
D. Walk in a straight line perpendicular to C's line.
E. Stay in line with C and D. E will trace the path of a sine curve as shown here:
What instructions could you give to five people to trace a cos(ine) curve?
What instructions could you give to five people to trace a tan(gent) curve?
Show answer & extension
Hide answer & extension
Cosine can be drawn the same way as sine but starting B at the top of the circle.
Tangent can be drawn by giving the following instructions:
A. Stand on the spot.
B. Walk around A in a circle, holding this string to keep you the same distance away.
C. Make a straight line with A and B, staying on the line tangent to the circle through B's starting point.
D. Walk in a straight line perpendicular to C's line.
E. Stay in line with C and D.
Could people be used to draw graphs of secant, cosecant and cotangent?
arccos + arcsin
What is the value of \(\arccos(x) + \arcsin(x)\)?
Show answer & extension
Hide answer & extension
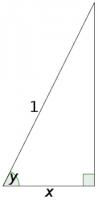
Let \(y = \arccos(x)\)
This means that \(x = \cos(y)\)
This gives us this triangle, as cosine is adjacent ÷ hypotenuse.
Call the angle at the top of the triangle \(z\).
Sine is opposite ÷ hypotenuse, so \(\sin(z) = x\)
So \(z = \arcsin(x)\)
Angles in triangle add to \(\pi\), so \(z = \frac{\pi}{2}-y\)
Hence, \(\arcsin(x)= \frac{\pi}{2}-y\)
Therefore \(\arccos(x) + \arcsin(x) = y + \frac{\pi}{2}-y\) \(=\frac{\pi}{2}\)
Extension
What are the values of \(\mathrm{arcsec}(x) + \mathrm{arccosec}(x)\) and \(\arctan(x) + \mathrm{arccot}(x)\)?
![](javascript:showlimage("cut-corn.png"))
![](javascript:showlimage("equal-side-and-angle.png"))
![](javascript:showlimage("three-squares.png"))
![](javascript:showlimage("sine4.gif"))
![](javascript:showlimage("cosine.gif"))
![](javascript:showlimage("tangent.gif"))
![](javascript:showlimage("arccos-triangle.png"))