Advent calendar 2024
8 December
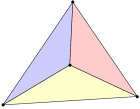
It is possible to arrange 4 points on a plane and draw non-intersecting lines
between them to form 3 non-overlapping triangles:
It is not possible to make more than 3 triangles with 4 points.
What is the maximum number of non-overlapping triangles that can be made by arranging 290 points on a plane
and drawing non-intersecting lines between them?
Show answer
Hide answer
By adding a point inside a triangle, you can turn one triangle into three triangles. By adding a point outside all the current triangles, you can add either
one or two more triangles. As we are after the maximum number of triangles, we will choose to add two triangles for each point we add.
Four points make 3 triangles. Adding 286 more points will add 572 more triangles, giving a total of 575.
![](javascript:showlimage("advent2024-8dec.png"))