Blog
2016-12-20
Last week, I posted about the Christmas card I designed on the Chalkdust blog.
![](javascript:showlimage("card2016.jpg"))
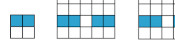
The card looks boring at first glance, but contains 12 puzzles. Converting the answers to base 3, writing them in the boxes on the front, then colouring the 1s green and 2s red will reveal a Christmassy picture.
If you want to try the card yourself, you can download this pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will be automatically converted to base 3 and coloured...
| # | Answer (base 10) | Answer (base 3) | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
- The square number larger than 1 whose square root is equal to the sum of its digits.
- The smallest square number whose factors add up to a different square number.
- The largest number that cannot be written in the form \(23n+17m\), where \(n\) and \(m\) are positive integers (or 0).
- Write down a three-digit number whose digits are decreasing. Write down the reverse of this number and find the difference. Add this difference to its reverse. What is the result?
- The number of numbers between 0 and 10,000,000 that do not contain the digits 0, 1, 2, 3, 4, 5 or 6.
- The lowest common multiple of 57 and 249.
- The sum of all the odd numbers between 0 and 66.
- One less than four times the 40th triangle number.
- The number of factors of the number \(2^{756}\)×\(3^{12}\).
- In a book with 13,204 pages, what do the page numbers of the middle two pages add up to?
- The number of off-diagonal elements in a 27×27 matrix.
- The largest number, \(k\), such that \(27k/(27+k)\) is an integer.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2016-12-20
@Matthew: Thank you for the prompt response! It makes sense now and perhaps I should have read a little closer!Dan Whitman
@Dan Whitman: Find the difference between the original number and the reverse of the original. Call this difference \(a\). Next add \(a\) to the reverse of \(a\)... ×1
Matthew
×1 In number 4 what are we to take the difference between? Do you mean the difference between the original number and its reverse? If so when you add the difference back to the reverse you simply get the original number, which is ambiguous. I am not sure what you are asking us to do here.
Dan Whitman
Add a Comment
2016-11-27
This year, the front page of mscroggs.co.uk will feature an advent calendar, just like last year. Behind each door, there will be a puzzle with a three digit solution. The solution to each day's puzzle forms part of a murder mystery logic puzzle in which you have to work out the murderer, motive, location and weapon used: the answer to each of these murder facts is a digit from 1 to 9 (eg. The murderer could be 6, the motive 9, etc.).
As you solve the puzzles, your answers will be stored in a cookie. Behind the door on Christmas Day, there will be a form allowing you to submit your answers. The winner will be randomly chosen from all those who submit the correct answer on Christmas Day. Runners up will then be chosen from those who submit the correct answer on Christmas Day, then those who submit the correct answer on Boxing Day, then the next day, and so on. As the winners will be chosen randomly, there is no need to get up at 5am on Christmas Day this year!
The winner will win this array of prizes:
![](javascript:showlimage("prizes2016.jpg"))
I will be adding to the pile of prizes throughout December. Runners up will get a subset of the prizes. The winner and runners up will also win an mscroggs.co.uk 2016 winners medal:
![](javascript:showlimage("medals2016.jpg"))
To win a prize, you must submit your entry before the end of 2016. Only one entry will be accepted per person. Once ten correct entries have been submitted, I will add a note here and below the calendar. If you have any questions, ask them in the comments below or on Twitter.
So once December is here, get solving! Good luck and have a very merry Christmas!
Edit: added picture of this year's medals.
Edit: more than ten correct entries have been submitted, list of prize winners can be found here.
You can still submit your answers but the only prize left is glory.
×1 (Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@Another Matthew: Ten correct submissions have been made. Just updating the pages to reflect this...
Matthew
Really enjoyed the extra bit at the end this year! Looking forward to 2017's calendar.
Louis
Add a Comment
2016-10-08
During my Electromagnetic Field talk this year, I spoke about @mathslogicbot (now reloated to @logicbot@mathstodon.xyz and @logicbot.bsky.social), my Twitter bot that is working its way through the tautologies in propositional calculus. My talk included my conjecture that the number of tautologies of length \(n\) is an increasing sequence (except when \(n=8\)). After my talk, Henry Segerman suggested that I also look at the number of contradictions of length \(n\) to look for insights.
A contradiction is the opposite of a tautology: it is a formula that is False for every assignment of truth values to the variables. For example, here are a few contradictions:
$$\neg(a\leftrightarrow a)$$
$$\neg(a\rightarrow a)$$
$$(\neg a\wedge a)$$
$$(\neg a\leftrightarrow a)$$
The first eleven terms of the sequence whose \(n\)th term is the number of contradictions of length \(n\) are:
$$0, 0, 0, 0, 0, 6, 2, 20, 6, 127, 154$$
This sequence is A277275 on OEIS. A list of contractions can be found here.
For the same reasons as the sequence of tautologies, I would expect this sequence to be increasing. Surprisingly, it is not increasing for small values of \(n\), but I again conjecture that it is increasing after a certain point.
Properties of the sequences
There are some properties of the two sequences that we can show. Let \(a(n)\) be the number of tautolgies of length \(n\) and let \(b(n)\) be the number of contradictions of length \(n\).
First, the number of tautologies and contradictions, \(a(n)+b(n)\), (A277276) is an increasing sequence. This is due to the facts that \(a(n+1)\geq b(n)\) and \(b(n+1)\geq a(n)\), as every tautology of length \(n\) becomes a contraction of length \(n+1\) by appending a \(\neg\) to be start and vice versa.
This implies that for each \(n\), at most one of \(a\) and \(b\) can be decreasing at \(n\), as if both were decreasing, then \(a+b\) would be decreasing. Sadly, this doesn't seem to give us a way to prove the conjectures, but it is a small amount of progress towards them.
Edit: Added Mastodon and Bluesky links
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-10-06
Thanks to Marc, I noticed that today's date is a palindrome in two different date formats—DMMYY (61016) and DMMYYYY (6102016).
This made me wonder when there will be another date that is palindromic in multiple date formats, so I wrote a Python script to find out.
Turns out there's not too long to wait: 10 July 2017 will be palindromic in two date formats (MDDYY and MDDYYYY). But before that, there's 1 July 2017, which is palindromic in three date formats (YYMMD, YYMD and MDYY). Most exciting of all, however, is 2 February 2020, which is palindromic in 7 different formats!
The next palindromic dates are shown in the following table. It will update as the dates pass.
| \(n\) | Next day with \(\geq n\) palindromic formats | Formats |
| 1 | 2 February 2026 | YYYYMDD |
| 2 | 2 June 2026 | YYMMD,YYMD,MDYY |
| 3 | 2 June 2026 | YYMMD,YYMD,MDYY |
| 4 | 2 March 2030 | YYYYMMDD,MMDDYYYY,YYYYMDD,MMDYY |
| 5 | 1 January 2110 | DDMYYYY,YYMDD,DDMYY,MMDYYYY,MMDYY |
| 6 | 1 January 2211 | YYMMD,DMYYYY,MDYYYY,YYMD,DMYY,MDYY |
A full list of future palindromic dates can be found here.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
In some of your full list you use the same format forwards and backwards. I'm just questioning why are YYMDD,DDMYY considered to be different formats when they are palendromic.
Stee
Add a Comment
2016-09-06
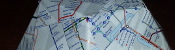
This is the fifth post in a series of posts about tube map folding.
After my talk at Electromagnetic Field 2014, I was sent a copy of
MC Escher Kaleidocycles by Doris Schattschneider and Wallace Walker (thanks Bob!).
A kaleidocycle is a bit like a 3D flexagon:
it can be flexed to reveal different parts of itself.
![](javascript:showlimage("kaleido.gif"))
In this blog post, I will tell you how to make a kaleidocycle from tube maps.
You will need
- 12 tube maps
- glue
Making the modules
First, fold the cover of a tube map over. This will allow you to have the tube
map (and not just its cover) on the faces of your shape.
![](javascript:showlimage("k1.jpg"))
![](javascript:showlimage("k2.jpg"))
With the side you want to see facing down, fold the map so that two
opposite corners touch.
![](javascript:showlimage("k3.jpg"))
For this step, there is a choice of which two corners to connect: leading to
a right-handed and a left-handed piece. You should make 6 of each type for your
kaleidocycle.
Finally, fold the overhanding bits over to complete your module.
![](javascript:showlimage("k4.jpg"))
![](javascript:showlimage("k5.jpg"))
The folds you made when connecting opposite corners will need to fold both
ways when you flex your shape, so it is worth folding them both ways a few times
now before continuing.
Putting it together
Once you have made 12 modules (with 6 of each handedness), you are ready
to put the kaleidocycle together.
Take two tube maps of each handedness and tuck them together in a line.
Each map is tucked into one of the opposite handedness.
![](javascript:showlimage("k5_.jpg"))
![](javascript:showlimage("k6.jpg"))
![](javascript:showlimage("k7.jpg"))
The four triangles across the middle form a net of a tetrahedron. Complete
the tetrahedron by putting the last tab into the first triangle. Glue these
together.
![](javascript:showlimage("k8.jpg"))
Take two more tube maps of the opposite handedness to those at the top of the tetrahedron.
Fit them into the two triangles poking out of the top of the tetrahedron to
make a second tetrahedron.
![](javascript:showlimage("k9.jpg"))
![](javascript:showlimage("k10.jpg"))
Repeat this until you have five connected tetrahedra. Finally, connect the
triangles poking out of the top and the bottom to make your kaleidocycle.
![](javascript:showlimage("kB.jpg"))
Previous post in series
This is the fifth post in a series of posts about tube map folding.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment