Puzzles
24 December
There are six ways to put two tokens in a 3 by 3 grid so that the diagonal from the top left to the bottom right is a line of symmetry:
Today's number is the number of ways of placing two tokens in a 29 by 29 grid so that the diagonal from the top left to the bottom right is a line of symmetry.
Show answer
Hide answer
Either both pieces must be on the diagonal, or one pieces is in the lower right half and the other is in the reflected position in the upper right half.
There are \(\left(\begin{array}{c}29\\2\end{array}\right)=406\) ways to pick two squares on the diagonal. There are 406 squares below the diagonal.
Therefore there are 406+406 = 812 ways to arrange the pieces.
23 December
198 is the smallest number that is equal to 11 times the sum of its digits.
Today's number is the smallest number that is equal to 48 times the sum of its digits.
Show answer
Hide answer
We're looking for a number \(n\) such that the digits of \(n\times48\) add up to \(n\). If we try numbers in order, we find that 9 works, so today's number is 432.
22 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number you can make with the digits in the red boxes.
| + | | + | | = 18 |
| + | | + | | + | |
| ÷ | | - | | = 1/2 |
| + | | + | | + | |
| + | | ÷ | | = 3/2 |
=
24 | | =
8 | | =
13 | |
Show answer
Hide answer
| 9 | + | 5 | + | 4 | = 18 |
| + | | + | | + | |
| 7 | ÷ | 2 | - | 3 | = 1/2 |
| + | | + | | + | |
| 8 | + | 1 | ÷ | 6 | = 3/2 |
=
24 | | =
8 | | =
13 | |
The largest number you can make with the digits in the red boxes is 984.
21 December
There are 3 ways to order the numbers 1 to 3 so that no number immediately follows the number one less that itself:
Today's number is the number of ways to order the numbers 1 to 6 so that no number immediately follows the number one less that itself.
Show answer
Hide answer
To make sequences of 4 numbers, we can insert 4s into three different places in the length 3 sequences given to obtain:
- 4, 3, 2, 1
- 3, 2, 4, 1
- 3, 2, 1, 4
- 4, 1, 3, 2
- 1, 4, 3, 2
- 1, 3, 2, 4
- 4, 2, 1, 3
- 2, 4, 1, 3
- 2, 1, 4, 3
There are some possibilities missing: those containing \(i, 4, i+1\). These can be found by taking the sequences of length 2, picking a number \(i\), adding 1 to every number larger than \(i\), then replacing \(i\) with \(i\ 4\ i+1\).
- 2, 1 → 3, 1 → 3, 1, 4, 2
- 2, 1 → 2, 1 → 2, 4, 3, 1
This gives a total of 3×3+2×1=11 sequences for 4 numbers.
To make sequences with 5 numbers, we can insert 5s into four different places in the length 4 sequences. This gives 4×11=44 sequences.
The missing sequences can then be found by taking the sequences of length 3, then doing the same process as above:
- 3, 2, 1 → 3, 2, 1 → 3, 5, 4, 2, 1
- 3, 2, 1 → 4, 2, 1 → 4, 2, 5, 3, 1
- 3, 2, 1 → 4, 3, 1 → 4, 3, 1, 5, 2
- 1, 3, 2 → 1, 4, 3 → 1, 5, 2, 4, 3
- 1, 3, 2 → 1, 3, 2 → 1, 3, 5, 4, 2
- 1, 3, 2 → 1, 4, 2 → 1, 4, 2, 5, 3
- 2, 1, 3 → 2, 1, 4 → 2, 5, 3, 1, 4
- 2, 1, 3 → 3, 1, 4 → 3, 1, 5, 2, 4
- 2, 1, 3 → 2, 1, 3 → 2, 1, 3, 5, 4
There are 3×3=9 of these, giving 44+9 = 53 total sequences of length 5.
To make sequences with 6 numbers, we can insert 6s into five different places in the length 5 sequences. This gives 5×53=265 sequences.
We can also make sequence by picking a number to replace in the length 4 sequences. This gives 4×11=44 more sequences.
Therefore there are 265+44 = 309 sequences in total.
20 December
18 can be written as the sum of 3 consecutive (strictly) positive integers: 5 + 6 + 7.
18 can also be written as the sum of 4 consecutive (strictly) positive integers: 3 + 4 + 5 + 6.
18 is in fact the smallest number that can be written as the sum of both 3 and 4 consecutive (strictly) positive integers.
Today's number is the smallest number that can be written as the sum of both 12 and 13 consecutive (strictly) positive integers.
Show answer
Hide answer
The sum of 13 consecutive integers is 13 times the middle number, so today's number is a multiple of 13.
The sum of 12 consecutive integers is 6 times the sum of the two middle numbers, so today's number is also a multiple of 6.
Therefore today's number is a multiple of 78.
78 and 156 do not work (the numbers would not all be strictly positive), so today's number is 234.
19 December
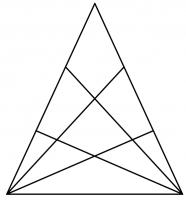
The diagram to the right shows a triangle. Two of the sides of the triangle have been split into three pieces, with lines drawn from the opposite vertex. In total, the diagram now contains 27 triangles of any size.
Another triangle has two of its sides split into eight pieces, with lines drawn from the opposite vertex. How many triangles (of any size) would this create?
Show answer
Hide answer
Each triangle must include one of the two corners at the base of the largest triangle (or both those corners).
To make triangles including the bottom left corner of the large triangle, we must pick two lines coming out of that corner, and one line coming out of the bottom right corner that is not the base of the triangle.
There are 9 lines coming out of the corners, so the total number of triangles is \(\left(\begin{array}{c}9\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=288\).
We now need to count the triangles that include the bottom right corner of the large triangle, but do not include both corners (as we've already counted thoses).
There are \(\left(\begin{array}{c}8\\2\end{array}\right)\times\left(\begin{array}{c}8\\1\end{array}\right)=224\) ways to pick lines to make these triangles.
In total, this makes 512 triangles.
18 December
The expansion of \((x+y+z)^3\) is
$$x^3 + y^3 + z^3 + 3x^2y + 3x^2z + 3xy^2 + 3y^2z + 3xz^2 + 3yz^2 + 6xyz.$$
This has 10 terms.
Today's number is the number of terms in the expansion of \((x+y+z)^{26}\).
Show answer
Hide answer
In each term, the powers of \(x\), \(y\) and \(z\) must add to 26: the terms will be of the form \(x^iy^jz^{26-i-j}\).
If \(i=0\), there are 27 choices for \(j\) (0 to 26).
If \(i=1\), there are 26 choices for \(j\) (0 to 25).
If \(i=2\), there are 25 choices for \(j\) (0 to 24).
...
If \(i=26\), there is 1 choice for \(j\) (0).
Therefore the total number of terms is 27+26+25+...+1 = 378.
17 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums and product are correct.
Today's number is the product of the numbers in the red boxes.
| + | | + | | = 16 |
| + | | + | | + | |
| + | | + | | = 8 |
| + | | + | | + | |
| × | | × | | = 288 |
=
11 | | =
14 | | =
20 | |
Show answer
Hide answer
| 6 | + | 3 | + | 7 | = 16 |
| + | | + | | + | |
| 1 | + | 2 | + | 5 | = 8 |
| + | | + | | + | |
| 4 | × | 9 | × | 8 | = 288 |
=
11 | | =
14 | | =
20 | |
The product of the numbers in the red boxes is 189.