Puzzles
14 December
The numbers 33, 404 and 311 contain duplicate digits. The numbers 120, 15 and 312 do not.
How many numbers between 10 and 999 (inclusive) contain no duplicate digits?
13 December
There are 6 ways to split the sequence of the numbers 1 to 5 into three shorter sequences:
- 1 and 2 and 3, 4, 5
- 1 and 2, 3 and 4, 5
- 1 and 2, 3, 4 and 5
- 1, 2 and 3 and 4, 5
- 1, 2 and 3, 4 and 5
- 1, 2, 3 and 4 and 5
Today's number is the number of ways to split the sequence of the numbers 1 to 10 into five shorter sequences.
12 December
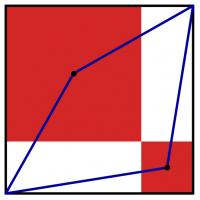
The diagram to the left shows a large black square. Inside this square, two red squares have been drawn.
(The sides of the red squares are parallel to the sides of the black square; each red square shares a vertex with the black square; and the two red squares share a vertex.)
A blue quadrilateral has then been drawn with vertices at two corners of the black square and the centres of the red squares.
The area of the blue quadrilateral is 167. What is the area of the black square?
11 December
Noel has a large pile of cards. Half of them are red, the other half are black. Noel splits the cards into two piles: pile A and pile B.
Two thirds of the cards in pile A are red. Noel then moves 108 red cards from pile A to pile B. After this move, two thirds of the cards in pile B are red.
How many cards did Noel start with?
Note: There was a mistake in the original version of today's puzzle. The number 21 has been replaced with 108.
10 December
Today's number is the smallest multiple of 24 whose digits add up to 24.
9 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | × | = 54 | |||
| × | + | ÷ | |||
| - | ÷ | = 1 | |||
| ÷ | - | × | |||
| + | - | = 6 | |||
| = 18 | = 6 | = 18 |
8 December
The residents of Octingham have 8 fingers. Instead of counting in base ten, they count in base eight: the digits of their numbers represent ones, eights, sixty-fours, two-hundred-and-fifty-sixes, etc
instead of ones, tens, hundreds, thousands, etc.
For example, a residents of Octingham would say 12, 22 and 52 instead of our usual numbers 10, 18 and 42.
Today's number is what a resident of Octingham would call 11 squared (where the 11 is also written using the Octingham number system).
7 December
There are 15 dominos that can be made using the numbers 0 to 4 (inclusive):
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
The sum of all the numbers on all these dominos is 60.
Today's number is the sum of all the numbers on all the dominos that can be made using the numbers 5 to 10 (inclusive).