Puzzles
Showing old puzzles. Show newest puzzles.
8 December
The residents of Octingham have 8 fingers. Instead of counting in base ten, they count in base eight: the digits of their numbers represent ones, eights, sixty-fours, two-hundred-and-fifty-sixes, etc
instead of ones, tens, hundreds, thousands, etc.
For example, a residents of Octingham would say 12, 22 and 52 instead of our usual numbers 10, 18 and 42.
Today's number is what a resident of Octingham would call 11 squared (where the 11 is also written using the Octingham number system).
Show answer
Hide answer
The Octingham resident's 11 is equal to our number 9. 9 squared is 81. 81 in base eight is 121.
Interestingly, this is the same answer as "just" doing 11 squred in base ten.
7 December
There are 15 dominos that can be made using the numbers 0 to 4 (inclusive):
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
The sum of all the numbers on all these dominos is 60.
Today's number is the sum of all the numbers on all the dominos that can be made using the numbers 5 to 10 (inclusive).
Show answer
Hide answer
Each number will appear 7 times: one time paired with the numbers six numbers 5 to 10, plus an extra appearance on the tile containing the same number twice.
The total of all the numbers is therefore 7×(5+6+...+10)=7×45=315.
6 December
There are 12 ways of placing 2 tokens on a 2×4 grid so that no two tokens are next to each other horizonally, vertically or diagonally:
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Today's number is the number of ways of placing 5 tokens on a 2×10 grid so that no two tokens are next to each other horizonally, vertically or diagonally.
Show answer
Hide answer
First, consider placing 5 tiles in a 1×9 grid. There is only one way to do this:
| O | O | O | O | O |
To get the number of ways of placing 5 tiles in a 1×10 grid, imagine adding an extra blank square to either the start or end of the grid or between two of the counters.
There are 6 places this tile could be inserted leading to 6 arrangements of 5 tiles in a 1×10 grid.
For 5 tiles in a 2×10 grid, you can first pick the columns the tiles go in (as a tile being in a column means nothing can be placed the columns either side, the number of ways to pick
columns is the same and the number of wats to arrange 5 tokens in a 1×10 grid). For each of these column choices, there are two locations for each tile (top or bottom).
This leads to a total number of arrangements of 6×25=192.
Tags: numbers, combinatorics
5 December
Carol rolled a large handful of six-sided dice. The total of all the numbers Carol got was 521. After some calculating, Carol worked out that the probability that of her total being 521
was the same as the probability that her total being 200. How many dice did Carol roll?
Show answer
Hide answer
The totals that are equally likely add up to 7 times the number of dice.
This can be seen by using the fact that the opposite sides of a dice add up to 7: for each way of making a given total with \(n\) dice, there is a way of making \(7n\) minus that total
by looking at the dice from below. Therefore \(T\) and \(7n-T\) are equally likely. (This also holds true (but is harder to explain) if you rearrange the faces of the dice so that the opposite
faces no longer add to 7.)
Therefore today's number is \((521+200)/7\), which is 103.
4 December
Today's number is a three digit number which is equal to the sum of the cubes of its digits. One less than today's number also has this property.
Show answer
Hide answer
If the final digit of the number is 0, then some carrying takes place when 1 is subtracted. Otherwise, no carrying happens.
If no carrying happens, call the three digits of today's number \(A\), \(B\), and \(C\). We know that \(A^3+B^3+C^3\) is one more than \(A^3 + B^3 + (C-1)^3\).
This implies that \(C^3=(C-1)^3+1\), which is only possible if \(C\) is 1.
Therefore either the final digit of today's number is 0 or the final digt of one less that today's number is 0. In both cases, we need to find a number
with the desired property whose final digit is 0: we are looking for digit \(A\) and \(B\) such that \(A^3+B^3\) is a multiple of 10.
Looking at all the cube numbers, there are a few combinations that add up to multiple of 10:
$$0^3+0^3=0$$
$$1^3+9^3=730$$
$$2^3+8^3=520$$
$$3^3+7^3=370$$
$$4^3+6^3=280$$
$$5^3+5^3=250$$
The only one of these that has the required property is 370. By checking 369 and finding it doesn't have the property, we see that the two numbers must be
370 and 371.
3 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number you can make with the digits in the red boxes.
| ÷ | - | = 3 | |||
| + | + | ÷ | |||
| ÷ | × | = 1 | |||
| × | - | + | |||
| - | × | = 20 | |||
| = 91 | = 6 | = 8 |
Show answer
Hide answer
| 9 | ÷ | 1 | - | 6 | = 3 |
| + | + | ÷ | |||
| 4 | ÷ | 8 | × | 2 | = 1 |
| × | - | + | |||
| 7 | - | 3 | × | 5 | = 20 |
| = 91 | = 6 | = 8 |
The largest number you can make with the digits in the red boxes is 321.
2 December
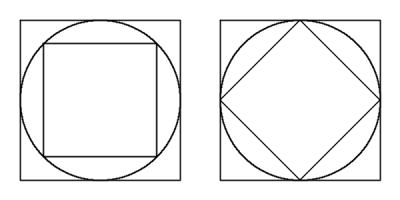
Carol draws a square with area 62. She then draws the smallest possible circle that this square is contained inside.
Next, she draws the smallest possible square that her circle is contained inside. What is the area of her second square?
Show answer
Hide answer
By drawing an appropriate diagram, it can be seen that the small square has half the area of the large square.
Therefore the area of the large square is 124.
1 December
It is possible to write 325 different numbers using the digits 1, 2, 3, 4, and 5 at most once each (and using no other digits).
How many of these numbers are odd?
Show answer
Hide answer
There are 3 one-digit numbers using these digits (1, 3 and 5).
To make two-digit odd numbers, there are 3 choices for the units digit, and 4 remaining choices for the tens digit.
To make three-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, and 3 remaining choices for the hundreds digit.
To make four-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, 3 remaining choices for the hundreds digit, and 2 remaining choices for the thousands digit.
To make five-digit odd numbers, there are 3 choices for the units digit, 4 remaining choices for the tens digit, 3 remaining choices for the hundreds digit, 2 remaining choices for the thousands digit and 1 remaining choice for the ten-thousands digit.
In total, this gives 3 + 3×4× + 3×4×3 + 3×4×3×2 + 3×4×3×2×1 = 195 odd numbers.
End of page. Show older puzzles.
Archive
Show me a random puzzle Most recent collections
Advent calendar 2024
Advent calendar 2023
Advent calendar 2022
Advent calendar 2021
List of all puzzles
Tags
sport multiples products cards trigonometry prime numbers rugby powers square roots chalkdust crossnumber polygons lines 2d shapes triangle numbers volume ave logic mean symmetry irreducible numbers rectangles gerrymandering quadratics fractions games indices factorials matrices complex numbers hexagons doubling combinatorics differentiation sums scales decahedra ellipses square numbers graphs angles digital products perfect numbers floors tiling dates cryptic clues cubics unit fractions menace geometric mean clocks square grids shape even numbers the only crossnumber calculus squares consecutive integers cube numbers dodecagons sequences time polynomials digits neighbours integration binary range consecutive numbers arrows crossnumbers books parabolas albgebra advent people maths medians remainders pascal's triangle quadrilaterals elections tangents coins perimeter taxicab geometry area regular shapes algebra dice pentagons multiplication means speed cryptic crossnumbers division money expansions geometric means grids integers star numbers chess triangles bases palindromes wordplay spheres balancing determinants number christmas folding tube maps numbers crosswords averages axes 3d shapes percentages dominos coordinates sets partitions odd numbers addition tournaments routes median sum to infinity factors planes proportion chocolate functions probability numbers grids digital clocks colouring surds probabilty geometry circles shapesArchive
Show me a random puzzle▼ show ▼ ▲ hide ▲
Most recent collections
Advent calendar 2024
Advent calendar 2023
Advent calendar 2022
Advent calendar 2021
List of all puzzles
Tags
crossnumbers functions taxicab geometry determinants probability digital clocks dice decahedra squares cryptic clues square numbers perimeter integration cubics factorials consecutive numbers indices games averages wordplay consecutive integers partitions axes menace planes powers regular shapes logic ellipses algebra angles christmas ave prime numbers the only crossnumber triangle numbers elections chess cryptic crossnumbers books doubling scales cards money grids odd numbers square roots digital products clocks expansions tiling time addition unit fractions balancing mean products spheres shape calculus chalkdust crossnumber differentiation median proportion digits sport dominos folding tube maps geometric means pascal's triangle perfect numbers numbers probabilty complex numbers irreducible numbers trigonometry star numbers dates routes quadrilaterals tournaments albgebra number remainders quadratics lines palindromes floors gerrymandering volume square grids integers coordinates circles rectangles pentagons means division symmetry parabolas bases sums sum to infinity geometry graphs neighbours binary percentages rugby triangles matrices coins fractions advent tangents sequences polynomials crosswords 3d shapes area people maths multiples range speed colouring hexagons shapes multiplication surds sets even numbers combinatorics geometric mean numbers grids dodecagons medians cube numbers chocolate 2d shapes factors polygons arrows© Matthew Scroggs 2012–2025