Puzzles
Equal lengths
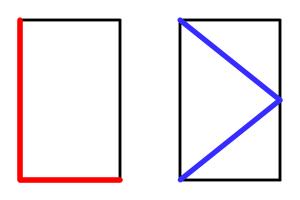
The picture below shows two copies of the same rectangle with red and blue lines. The blue line visits the midpoint of the opposite side. The lengths shown in red and blue are of equal length.
What is the ratio of the sides of the rectangle?
Show answer
Hide answer
Let \(a\) be the height of the rectangle and \(b\) be the width.
The length of the red line is \(a+b\). The length of the blue line is \(2\sqrt{a^2+\frac{b^2}4}\). These are equal so:
\begin{align}
a+b&=2\sqrt{a^2+\frac{b^2}4}\\
(a+b)^2&=4\left(a^2+\frac{b^2}{4}\right)\\
a^2+2ab+b^2&=4a^2+b^2\\
0&=3a^2-2ab\\
0&=3a-2b\\
2b&=3a
\end{align}
Therefore the ratio of the sides is 2:3.
Is it equilateral?
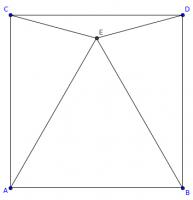
In the diagram below, \(ABDC\) is a square. Angles \(ACE\) and \(BDE\) are both 75°.
Is triangle \(ABE\) equilateral? Why/why not?
Show answer
Hide answer
The triangle is equilateral.
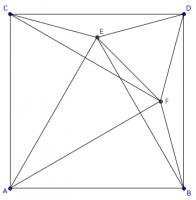
To see why, add a copy of point \(E\) rotated by 90°. This is labelled \(F\) on the diagram below.
Angles \(BDE\) and \(CDF\) are both 75°. Therefore angles \(CDE\) and \(BDF\) are both 15°. This means that angle \(FDE\) is 60°.
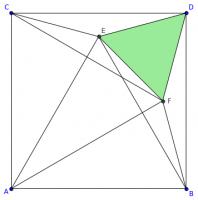
Line \(AD\) is a line of symmetry of the diagram, so angles \(DFE\) and \(DEF\) are equal and both 60°. Therefore, triangle DEF is equilateral. This triangle is show in green in the diagram below.
Lines \(EF\), \(DF\) and \(BF\) are all equal length, so triangles \(BFE\) and \(BFD\) are isosceles.
Angles \(BDF\) and \(FBD\) are both 15°. Angles \(FBE\) and \(FEB\) are equal, and the angles in triangle \(BED\) add to 180°: this means that angle \(FBE\) is 15°.
Angles \(FBE\) and \(FBD\) are both 15°, and so angle \(EBD\) is 30°. Angles \(EBD\) and \(ABE\) add to 90°, and so angle \(ABE\) is 60°.
By symmetry, angle \(BAE\) is also 60°. Angle \(BEA\) must therefore also be 60°, so triangle \(ABE\) is equilateral.
Bending a straw
Two points along a drinking straw are picked at random. The straw is then bent at these points. What is the probability that the two ends meet up to make a triangle?
Show answer & extension
Hide answer & extension
A triangle will be made if none of the segments of straw is longer than the other two added together. This is the same as requiring that each segment must be less than half the straw.
Let the length of the straw be 1 unit. Call the points \(x\) and \(y\). A triangle is made if either:
- \(x\lt y\), \(x\lt\tfrac12\), \(y-x\lt\tfrac12\), \(1-y\lt\tfrac12\); or
- \(y\lt x\), \(y\lt\tfrac12\), \(x-y\lt\tfrac12\), \(1-x\lt\tfrac12\).
For the second condition, the allowable region is shown below.
This region covers \(\tfrac18\) of the whole square. By switching \(x\) and \(y\) it can be seen that the first condition's region is the same size as the second's, plus they don't overlap. Therefore the probability of making a triangle is \(\tfrac18+\tfrac18=\tfrac14\).
Extension
One point along a drinking straw is picked, then a coin is flipped. If the coin shows heads, a second point above the first is chosen; If tails, a second point below the first is chosen. The straw is then bent at these points. What is the probability that the two ends meet up to make a triangle?
Placing plates
Two players take turns placing identical plates on a square table. The player who is first to be unable to place a plate loses. Which player wins?
Show answer & extension
Hide answer & extension
The first player can always win by first placing a plate on the exact centre of the table. Then the first player can copy what the second player does, but rotated 180°, and hence can always place a plate if the second player could.
Extension
What if the two players play on a regular hexagonal table? Or a regular octagonal table? Or a regular pentagonal table? Or a regular \(n\)-gonal table?
20 December
Start with a line of length 2. Draw a line of length 17 perpendicular to it. Connect the ends to make a right-angled triangle.
The length of the hypotenuse of this triangle will be a non-integer.
Draw a line of length 17 perpendicular to the hypotenuse and make another right-angled triangle. Again the new hypotenuse will have a non-integer length.
Repeat this until you get a hypotenuse of integer length. What is the length of this hypotenuse?
17 December
The number of degrees in one internal angle of a regular polygon with 360 sides.
3 December
What is the volume of the smallest cube inside which a rectangular-based pyramid of volume 266 will fit?
2 December
What is the maximum number of lines that can be formed by the intersection
of 30 planes?
![](javascript:showlimage("rectangles506.png"))
![](javascript:showlimage("square-cd07.png"))
![](javascript:showlimage("square-cd07-sol1.png"))
![](javascript:showlimage("square-cd07-sol2.png"))
![](javascript:showlimage("straws_1.png"))
