Puzzles
Multiples of three
If the digits of a number add up to a multiple of three, then the number is a multiple of three. Therefore if a two digit number, \(AB\) (first digit \(A\), second digit \(B\); not \(A\times B\)), is a multiple of three, then \(A0B\) is also a multiple of three.
If \(AB\div 3=n\), then what is \(A0B\div 3\)?
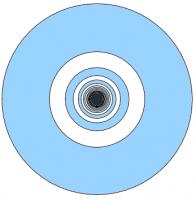
Dartboard
Concentric circles with radii 1, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), ... are drawn. Alternate donut-shaped regions are shaded.
What is the total shaded area?
Show answer & extension
Hide answer & extension
The shaded area is:
$$\pi (1)^2 - \pi (\frac{1}{2})^2 + \pi (\frac{1}{3})^2 - \pi (\frac{1}{4})^2 + \pi (\frac{1}{5})^2 - ...$$
$$=\sum_{i=1}^\infty \frac{\pi (-1)^{i-1}}{i^2}$$
$$=\pi\sum_{i=1}^\infty \frac{(-1)^{i-1}}{i^2}$$
$$=\pi\left(\frac{\pi^2}{12}\right)$$
$$=\frac{\pi^3}{12}$$
Extension
Prove that
$$=\sum_{i=1}^\infty \frac{(-1)^{i-1}}{i^2}=\frac{\pi^2}{12}$$
Seven digits
"I'm thinking of a number. I've squared it. I've squared the square. And I've multiplied the second square by the original number. So I now have a number of seven digits whose final digit is a 7," said Dr. Dingo to his daughter.
Can you work out Dr. Dingo's number?
Show answer & extension
Hide answer & extension
Let's call Dr. Dingo's number \(n\). If the number is squared twice then multiplied by \(n\), we get \(n^5\).
For all integers \(n\), the final digit of \(n^5\) is the same as the final digit of \(n\). In other words:
$$n^5\equiv n \mod 10$$
Therefore, the final digit of Dr. Dingo's number is 7.
$$7^5=16807$$
$$17^5=1419857$$
$$27^5=14348907$$
So, in order for the answer to have seven digits, Dr. Dingo's number was 17.
Extension
For which integers \(m\) does there exist an integer \(n\) such that for all integers \(x\):
$$x^n\equiv x \mod m$$
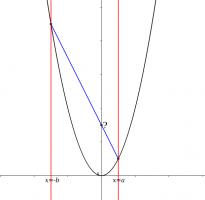
Parabola
On a graph of \(y=x^2\), two lines are drawn at \(x=a\) and \(x=-b\) (for \(a,b>0\). The points where these lines intersect the parabola are connected.
What is the y-coordinate of the point where this line intersects the y-axis?
Show answer & extension
Hide answer & extension
The co-ordinates of the points where the lines intersect the parabola are \((a,a^2)\) and \((-b,b^2)\). Hence the gradient of the line between them is:
$$\frac{a^2-b^2}{a-(-b)}=\frac{(a+b)(a-b)}{a+b}=a-b$$
Therefore the y-coordinate is:
$$b^2 + b(a-b) = ba$$
Ferdinand Möbius, who discovered this property called the curve a Multiplicationsmaschine or 'multiplication machine' as it could be used to perform multiplication.
Extension
How could you use the graph of \(y=x^2\) to divide 100 by 7?
Differentiate this
$$f(x)=e^{x^{ \frac{\ln{\left(\ln{x}\right)}}{ \ln{x}}} }$$
Find \(f'(x)\).
Show answer
Hide answer
$$f(x)=e^{x^{ \frac{\ln{\left(\ln{x}\right)}}{ \ln{x}}} }$$
$$=e^{e^{ \frac{\ln{\left(\ln{x}\right)}}{ \ln{x}}\ln{x}} }$$
$$=e^{e^{ \ln{\left(\ln{x}\right)}} }$$
$$=e^{\ln{x} }$$
$$=x$$
Therefore:
$$f'(x)=1$$
Square numbers
Towards the end of his life, Lewis Carroll recorded in his diary that he had discovered that double the sum of two square numbers could always be written as the sum of two square numbers. For example
$$2(3^2 +4^2 )=1^2 +7^2$$
$$2(5^2 +8^2 )=3^2 +13^2$$
Prove that this can be done for any two square numbers.
Show answer & extension
Hide answer & extension
Let \(a^2\) and \(b^2\) be the two square numbers.
$$2(a^2 +b^2 ) = 2a^2 +2b^2$$
$$= a^2 + 2ab + b^2 + a^2 - 2ab + b^2$$
$$= (a+b)^2 +(a-b)^2$$
Extension
Prove that 3 times the sum of 3 squares is also the sum of 4 squares.
N
Consider three-digit integers \(N\) such that:
(a) \(N\) is not exactly divisible by 2, 3 or 5.
(b) No digit of \(N\) is exactly divisible by 2, 3 or 5.
How many such integers \(N\) are there?
Show answer & extension
Hide answer & extension
(b) implies that the digits of \(N\) are all 1 or 7, so \(N\) can only be 111, 117, 171, 177, 711, 717, 771 or 777. These are all divisible by 3, so no such integers \(N\) exist.
Extension
Consider 21-digit integers \(N\) such that:
(a) \(N\) is not exactly divisible by 2, 3 or 5.
(b) No digit of \(N\) is exactly divisible by 2, 3 or 5.
How many such integers \(N\) are there?
MathsJam
Maths Jam is always held on the second-to-last Tuesday of the month. This month, it will be held on the 17th. What is the earliest date in the month on which Maths Jam can fall and when will this next happen?