Puzzles
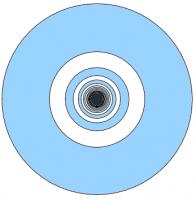
Dartboard
Concentric circles with radii 1, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), ... are drawn. Alternate donut-shaped regions are shaded.
What is the total shaded area?
If you enjoyed this puzzle, check out Sunday Afternoon Maths XIX,
puzzles about 2d shapes, or a random puzzle.
puzzles about 2d shapes, or a random puzzle.