Sunday Afternoon Maths XIX
Posted on 2014-06-29
Multiples of three
If the digits of a number add up to a multiple of three, then the number is a multiple of three. Therefore if a two digit number, \(AB\) (first digit \(A\), second digit \(B\); not \(A\times B\)), is a multiple of three, then \(A0B\) is also a multiple of three.
If \(AB\div 3=n\), then what is \(A0B\div 3\)?
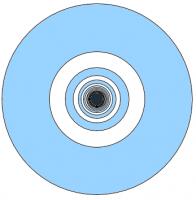
Dartboard
Concentric circles with radii 1, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), ... are drawn. Alternate donut-shaped regions are shaded.
What is the total shaded area?
If you enjoyed these puzzles, check out Advent calendar 2025,
puzzles about probability, or a random puzzle.
puzzles about probability, or a random puzzle.