Puzzles
Showing old puzzles. Show newest puzzles.
Odd and even outputs
Let \(g:\mathbb{N}\times\mathbb{N}\rightarrow\mathbb{N}\) be a function.
This means that \(g\) takes two natural number inputs and gives one natural number output. For example if \(g\) is defined by \(g(n,m)=n+m\) then \(g(3,4)=7\) and \(g(10,2)=12\).
The function \(g(n,m)=n+m\) will give an even output if \(n\) and \(m\) are both odd or both even and an odd output if one is odd and the other is even. This could be summarised in the following table:
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | odd |
| e | odd | even | |
Using only \(+\) and \(\times\), can you construct functions \(g(n,m)\) which give the following output tables:
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Show answer & extension
Hide answer & extension
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | odd | odd |
| e | odd | odd | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | odd | odd |
| e | odd | even | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | odd | odd |
| e | even | odd | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | odd | odd |
| e | even | even | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | odd | even |
| e | odd | odd | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | odd | even |
| e | odd | even | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | odd | even |
| e | even | odd | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | odd | even |
| e | even | even | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | odd |
| e | odd | odd | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | odd |
| e | odd | even | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | odd |
| e | even | odd | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | odd |
| e | even | even | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | even |
| e | odd | odd | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | even |
| e | odd | even | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | even |
| e | even | odd | |
| \(n\) | |||
| odd | even | ||
| \(m\) | odd | even | even |
| e | even | even | |
Extension
Can you find functions \(h:\mathbb{N}\times\mathbb{N}\times\mathbb{N}\rightarrow\mathbb{N}\) (call the inputs \(n\), \(m\) and \(l\)) to give the following outputs:
|
| ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
etc
Tags: functions
Twenty-one
Scott and Virgil are playing a game. In the game the first player says 1, 2 or 3, then the next player can add 1, 2 or 3 to the number and so on. The player who is forced to say 21 or above loses. The first game went like so:
Scott: 3
Virgil: 4
Scott: 5
Virgil: 6
Scott: 9
Virgil: 12
Scott: 15
Virgil 17
Scott: 20
Virgil: 21
Virgil loses.
To give him a better chance of winning, Scott lets Virgil choose whether to go first or second in the next game. What should Virgil do?
Show answer & extension
Hide answer & extension
Virgil should go second. Whatever Scott adds, Virgil should then add to make four. For example, if Scott says 3, Virgil should say 1.
Using this strategy, Virgil will say 4, 8, 12, 16 then 20, forcing Scott to go above 21.
Extension
(i) If instead of 21, 22 cannot be said/beaten, how should Virgil win? How about 23? Or 24? How about \(n\)?
(ii) If instead of adding 1 to 3, 1 to 4 can be added, how should Virgil win? How about 1 to 5? Or 2 to 5? How about \(m\) to \(l\)?
(iii) Alan wants to join the game. Can Virgil win if there are three people? Can he win if there are \(k\) people?
Polya strikes out
Write the numbers 1, 2, 3, ... in a row. Strike out every third number beginning with the third. Write down the cumulative sums of what remains:
1, 2, 3, 4, 5, 6, 7, ...
1, 2, 3, 4, 5, 6, 7, ...
1, 2, 4, 5, 7, ...
1=1; 1+2=3; 1+2+4=7; 1+2+4+5=12; 1+2+4+5+7=19; ...
1, 3, 7, 12, 19, ...
Now strike out every second number beginning with the second. Write down the cumulative sums of what remains. What is the final sequence? Why do you get this sequence?
Show answer & extension
Hide answer & extension
1, 3, 7, 12, 19, ...
1, 7, 19, ...
1=1; 1+7=8; 1+7+19=27; ...
1, 8, 27, ...
The final sequence is the cube numbers. To show why, let \(n\) be an integer and follow through the process.
Cross out every third number:
1, 2, 3, 4, 5, 6, ..., 3n, \(3n+1\), \(3n+2\), ...
1, 2, 4, 5, ..., \(3n+1\), \(3n+2\), ...
Find the cumulative sums:
$$1=1$$
$$1+2=1+2=3$$
$$1+2+4=1+2+3+4-3=7$$
$$1+2+4+5=1+2+3+4+5-3=12$$
$$...$$
$$1+2+4+5+...+(3n+1)=\sum_{i=1}^{3n+1}-\sum_{i=1}^{n}3i$$
$$=\frac{1}{2}(3n+1)(3n+2)-\frac{3}{2}n(n+1)$$
$$=3n^2+3n+1$$
$$1+2+4+5+...+(3n+2)=3n^2+3n+1+(3n+2)$$
$$=3n^2+6n+3$$
$$...$$
1, 3, 7, 12, ..., \(3n^2+3n+1\), \(3n^2+6n+3\), ...
Cross out every second number, starting with the second:
1, 3, 7, 12, ..., \(3n^2+3n+1\), 3n2+6n+3, ...
1, 7, ..., \(3n^2+3n+1\), ...
Find the cumulative sums. The \(m\)th sum is:
$$\sum_{n=0}^{m}3n^2+3n+1$$
$$=3\sum_{n=0}^{m}n^2+3\sum_{n=0}^{m}n+\sum_{n=0}^{m}1$$
$$=\frac{3}{6}m(m+1)(2m+1)+\frac{3}{2}m(m+1)+m+1$$
$$=\frac{1}{2}(m+1)(m(2m+1)+3m+2)$$
$$=\frac{1}{2}(m+1)(2m^2+m+3m+2)$$
$$=\frac{1}{2}(m+1)(2m^2+4m+2)$$
$$=(m+1)(m^2+2m+1)$$
$$=(m+1)(m+1)^2$$
$$=(m+1)^3$$
Hence the numbers obtained are the cube numbers.
Extension
What happens if you cross out every third number starting at the second? Or every fifth number starting at the fifth? Or every \(n\)th number starting at the \(m\)th?
Tags: numbers
Whist
Messrs. Banker, Dentist, Apothecary and Scrivener played whist last night. (whist is a four player card game where partners sit opposite each other.) Each of these gentlemen is the namesake of another's vocation.
Last night, the apothecary partnered Mr. Apothecary; Mr. Banker's partner was the scrivener; on Mr. Scrivener's right sat the dentist.
Who sat on the banker's left?
Show answer & extension
Hide answer & extension
Represent each player by a compass point. Let B, D, A and S represent Messrs. Banker, Dentist, Apothecary and Scrivener respectively and b, d, a and s represent the four jobs.
Mr. Banker (B) partners the scrivener (s). Let B sit at West. This means s sits at East. As no other player can also be B or s, the table looks like this:
| ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||
| ||||||||||||||||||||||||||
The dentist (d) sits on Mr. Scrivener's (S) right. East cannot be S, so North cannot be d. East cannot be d, so South cannot be S.
| ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||
| ||||||||||||||||||||||||||
By elimination, only North can be S. This means that d must sit to the right of North (at West):
| ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||
| ||||||||||||||||||||||||||
A and a are partners. This is only possible if A is South and a is North:
| ||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||
| ||||||||||||||||||||||||||
Therefore, Mr. Banker the dentist sits to the left of the banker.
Extension
If each person is partnered with their job namesake, how many possible combinations of names and jobs are possible?
Exact change
Source: @AlexDBolton on Twitter
In the UK, the coins less than £1 are 1p, 2p, 5p, 10p, 20p and 50p. How many coins would I need to carry in my pocket so that I could make any value from 1p to 99p?
In the US, the coins less than $1 are 1¢, 5¢, 10¢, 25¢. How many coins would I need to carry in my pocket so that I could make any value from 1¢ to 99¢?
Show answer & extension
Hide answer & extension
In the UK, eight coins are needed: 1p, 1p, 2p, 5p, 10p, 20p, 20p, 50p.
In the US, ten coins are needed: 1¢, 1¢, 1¢, 1¢, 5¢, 10¢, 10¢, 25¢, 25¢, 25¢.
Extension
In a far away country, the unit of currency is the #, which is split into 100@ (# is like £ or $; @ is like p or ¢).
Let C be the number of coins less than #1. Let P be the number of coins needed to make any value between 1@ and 99@. Which coins should be the country mint to minimise the value of P+C?
Square cross
Source: Teach Further Maths Blog
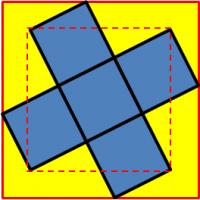
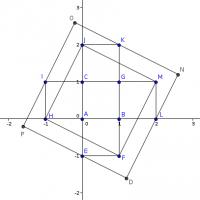
A figure in the shape of a cross is made from five 1 x 1 squares, as shown. The cross is inscribed in a large square whose sides are parallel to the dashed square, formed by four vertices of the cross.
What is the area of the large outer square?
Show answer
Hide answer
The smaller diagonal square is made up of a 1×1 square and four 1×2 right-angled triangles. Therefore its area is 5.
The line FM, and therefore the line DN, has gradient 2. The line JM, and therefore the line ON, has gradient -½. ON passes through (1,2) and DN passes through (2,0). Therefore, DN has equation \(y=2x-4\) and ON has equation \(y=\frac{5}{2}-\frac{1}{2}x\). These lines intersect at \((\frac{13}{5},\frac{6}{5})\), these are the co-ordinates of N. By the same method, the co-ordinates of P are \((-\frac{8}{5},-\frac{1}{5})\).
By Pythagoras' Theorem, The diagonal of the larger square is \(\frac{7\sqrt{10}}{5}\) and so the area of the larger square is 9.8.
Ten digit number
Source: Richard Wiseman's Blog
Can you create a 10-digit number, where the first digit is how many zeros in the number, the second digit is how many 1s in the number etc. until the tenth digit which is how many 9s in the number?
Show answer & extension
Hide answer & extension
6210001000 has 6 zeros, 2 ones, 1 two, 0 threes, 0 fours, 0 fives, 1 six, 0 sevens, 0 eights and 0 nines.
Extension
Are there any more numbers like this? Prove that you have them all.
Tags: numbers
Mrs. Coldcream objected
"I object," said Councillor Mrs. Coldcream. "I see no reason why the boys should be so favoured at the expense of the girls."
This was at a meeting of the Holmshire Education Committee. It had been proposed to award 19 scholarships totalling £1000 to boys and girls of the county. It had been proposed that each girl receive a set amount and each boy receive £30 more than each girl.
Mrs. Coldcream pressed her point with such fervour that it was decided to reallocate the money. Each girl would receive £8 more than originally proposed, with the boys' scholarships scaled down accordingly.
How much did each boy and each girl receive?
Show answer & extension
Hide answer & extension
Let \(G\) be the number of girls, and £\(x\) be the amount each girl was originally to receive. This means that there are \(19-G\) boys who were to receive £\(x+30\). The total scholarship is £1000, so:
$$xG+(x+30)(19-G)=1000$$
This simplifies to:
$$19x-30G=430$$
\(G\) is less than 19, so the only integer solution of this equation is \(x=40\) and \(G=11\).
After the funds are redistributed, each girl therefore receives £48. Let \(B\) be the amount each boy will now receive. The total is still £1000, so:
$$48\times 11+8B=1000$$
Which can be solved to find \(B=59\).
Each girl receives £48 and each boy receives £59.
Extension
Mrs. Coldcream still feels that this is unfair. How much more should be added to each girl's scholarship (resizing the boys' accordingly) so that the girls get at least as much as the boys?
Tags: numbers
End of page. Show older puzzles.
Archive
Show me a random puzzle Most recent collections
Advent calendar 2024
Advent calendar 2023
Advent calendar 2022
Advent calendar 2021
List of all puzzles
Tags
neighbours crossnumbers star numbers factorials time prime numbers averages elections geometric mean regular shapes even numbers percentages irreducible numbers planes consecutive integers numbers the only crossnumber 3d shapes indices chess number cryptic clues digits floors perimeter partitions symmetry advent coordinates median triangles sequences quadratics pascal's triangle geometry square roots range algebra triangle numbers balancing logic decahedra cubics speed polygons functions differentiation matrices perfect numbers combinatorics arrows binary trigonometry quadrilaterals probability division tournaments odd numbers numbers grids complex numbers integers colouring folding tube maps consecutive numbers parabolas integration addition multiplication remainders digital clocks chalkdust crossnumber circles shape coins rugby lines proportion doubling unit fractions taxicab geometry probabilty chocolate sets people maths determinants axes wordplay sums scales square grids expansions pentagons books powers cards menace routes calculus grids surds digital products geometric means albgebra factors money squares hexagons means ellipses graphs mean cryptic crossnumbers tangents dates games medians multiples crosswords dodecagons christmas fractions cube numbers sport tiling square numbers rectangles bases products dice sum to infinity spheres ave palindromes shapes volume dominos polynomials angles gerrymandering 2d shapes clocks areaArchive
Show me a random puzzle▼ show ▼ ▲ hide ▲
Most recent collections
Advent calendar 2024
Advent calendar 2023
Advent calendar 2022
Advent calendar 2021
List of all puzzles
Tags
circles consecutive integers advent polynomials range neighbours square roots factorials prime numbers proportion dice odd numbers cards powers fractions crosswords rugby numbers grids pentagons triangle numbers scales trigonometry integration parabolas the only crossnumber dodecagons probability sport graphs dates cryptic clues tournaments palindromes elections factors coordinates bases coins triangles colouring christmas medians shape means crossnumbers geometry arrows median geometric mean mean even numbers money doubling probabilty books routes unit fractions star numbers surds ellipses menace perfect numbers perimeter pascal's triangle multiples partitions albgebra logic sum to infinity people maths spheres lines hexagons angles area percentages cube numbers 3d shapes sums squares averages chalkdust crossnumber chess cryptic crossnumbers axes expansions rectangles consecutive numbers chocolate shapes 2d shapes grids sets binary functions volume dominos quadratics algebra number speed determinants geometric means folding tube maps combinatorics games gerrymandering polygons tiling floors taxicab geometry sequences digits complex numbers balancing planes multiplication division decahedra irreducible numbers symmetry regular shapes matrices numbers square grids time differentiation square numbers wordplay digital clocks remainders digital products calculus products integers addition indices cubics quadrilaterals tangents clocks ave© Matthew Scroggs 2012–2025