Sunday Afternoon Maths XXXIV
Find them all
Find all continuous positive functions, \(f\) on \([0,1]\) such that:
$$\int_0^1 f(x) dx=1\\
\mathrm{and }\int_0^1 xf(x) dx=\alpha\\
\mathrm{and }\int_0^1 x^2f(x) dx=\alpha^2$$
Show answer & extension
Hide answer & extension
$$0=\alpha^2-2\alpha^2+\alpha^2\\
=\int_0^1 x^2f(x) dx-2\int_0^1 \alpha xf(x) dx+\int_0^1 \alpha^2f(x)dx\\
=\int_0^1 (x^2-2\alpha x+\alpha^2)f(x)dx\\
=\int_0^1 (x-\alpha)^2 f(x)dx$$
\(f(x)\) and \((x-\alpha)^2\) are both positive so this is only possible if one of them if always zero.
But \((x-\alpha)^2\) is only zero when \(x=\alpha\) and \(\int_0^1 f(x) dx=1\) so \(f(x)\) cannot always be zero. Therefore no such function exists.
Extension
Find all continuous positive functions, \(f\) on \([0,1]\) such that:
$$\int_0^1 f(x) dx=1\\
\int_0^1 xf(x) dx=1\\$$
Four points on a shape
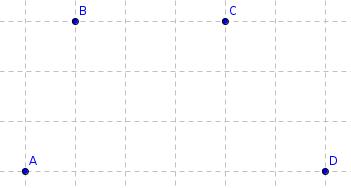
Fiona wants to draw a 2-dimensional shape whose perimeter passes through the points A, B, C and D
Which of the following shapes can she draw?
(i) A circle
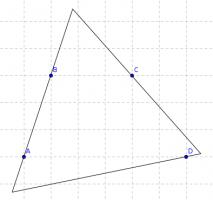
(ii) An equilateral triangle
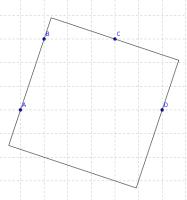
(iii) A square
Show answer & extension
Hide answer & extension
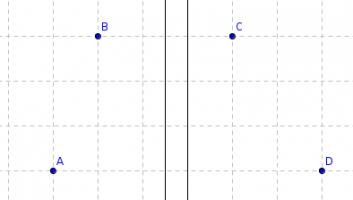
(i) If a circle could be drawn, then its centre would be equidistant from each pair of points. But the locus of points equidistant from B and C is parallel to the locus of points equidistant from A and D.
Therefore it is impossible to place the centre of the circle, so no circle can be drawn.
(ii)
(iii)
Extension
Let A, B, C and D be any four points. When is it possible to draw
(i) A circle
(ii) An equilateral triangle
(iii) A square
through the four points?
Algebraic fractions
Given that
$$\frac{3x+y}{x-3y}=-1$$
what is the value of
$$\frac{x+3y}{3x-y}$$
?
Show answer & extension
Hide answer & extension
$$\frac{3x+y}{x-3y}=-1$$
implies that
$$3x+y=3y-x\\
2x=y$$
This means that
$$\frac{x+3y}{3x-y}=\frac{x+6x}{3x-2x}\\
=\frac{7x}{x}\\=7$$
Extension
Given that
$$\frac{3x+y}{x-3y}=-k$$
what is the value of
$$\frac{x+3y}{3x-y}$$
?
For which values of \(k\) is the answer an integer?
Four integers
\(a\), \(b\), \(c\) and \(d\) are four positive (and non-zero) integers.
$$abcd+abc+bcd+cda+dab+ab+bc+cd+da+ac+bd\\+a+b+c+d=2009$$
What is the value of \(a+b+c+d\)?
Show answer & extension
Hide answer & extension
$$abcd+abc+bcd+cda+dab+ab+bc+cd+da+ac+bd\\+a+b+c+d=(a+1)(b+1)(c+1)(d+1)-1$$
So:
$$(a+1)(b+1)(c+1)(d+1)=2010\\=2\times 3\times 5\times 67$$
Therefore \(a+b+c+d=1+2+4+66=73\).
Extension
Which numbers could 2009 be replaced with so that the problem still has a unique solution?
Sum
What is
$$\sum_{i=1}^{\infty}\frac{1}{i 2^i}$$
?
Show answer & extension
Hide answer & extension
Write \(x\) instead of 2. Now we find that:
$$\frac{d}{dx}\sum_{i=1}^{\infty}\frac{1}{i x^i}=\sum_{i=1}^{\infty}\frac{-1}{x^{i+1}}\\
=-\frac{1}{x}\sum_{i=1}^{\infty}\frac{1}{x^i}\\
=-\frac{1}{x}\times\frac{1}{x-1}\\
=\frac{1}{x}+\frac{1}{1-x}$$
The sum we are after is the integral of this:
$$\sum_{i=1}^{\infty}\frac{1}{i x^i}=\ln|x|+\ln|1-x|$$
When \(x=2\), this is \(\ln(2)\)
Extension
What is
$$\sum_{i=1}^{\infty}\frac{1}{i^2 2^i}$$
?
![](javascript:showlimage("four-points.png"))
![](javascript:showlimage("four-points-circle.png"))
![](javascript:showlimage("four-points-triangle.png"))
![](javascript:showlimage("four-points-square.png"))