Sunday Afternoon Maths XXVIII
Posted on 2014-09-14
The ace of spades
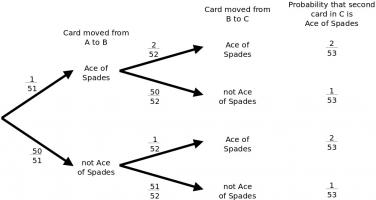
I have three packs of playing cards with identical backs. Call the packs A, B and C.
I draw a random card from pack A and shuffle it into pack B.
I now turn up the top card of pack A, revealing the Queen of Hearts.
Next, I draw a card at random from pack B and shuffle it into pack C. Then, I turn up the top card of pack B, revealing another Queen of Hearts.
I now draw a random card from pack C and place it at the bottom of pack A.
What is the probability that the card at the top of pack C is the Ace of Spades?
3n+1
Let \(S=\{3n+1:n\in\mathbb{N}\}\) be the set of numbers one more than a multiple of three.
(i) Show that \(S\) is closed under multiplication.
ie. Show that if \(a,b\in S\) then \(a\times b\in S\).
Let \(p\in S\) be irreducible if \(p\not=1\) and the only factors of \(p\) in \(S\) are \(1\) and \(p\). (This is equivalent to the most commonly given definition of prime.)
(ii) Can each number in \(S\) be uniquely factorised into irreducibles?
2009
Source: Teaching Further Maths blog
2009 unit cubes are glued together to form a cuboid. A pack, containing 2009 stickers, is opened, and there are enough stickers to place 1 sticker on each exposed face of each unit cube.
How many stickers from the pack are left?
If you enjoyed these puzzles, check out Advent calendar 2024,
puzzles about cryptic crossnumbers, or a random puzzle.
puzzles about cryptic crossnumbers, or a random puzzle.