Puzzles
The ace of spades
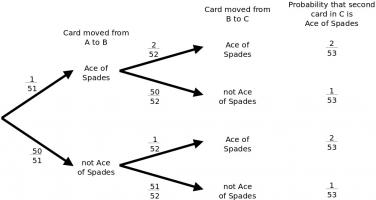
I have three packs of playing cards with identical backs. Call the packs A, B and C.
I draw a random card from pack A and shuffle it into pack B.
I now turn up the top card of pack A, revealing the Queen of Hearts.
Next, I draw a card at random from pack B and shuffle it into pack C. Then, I turn up the top card of pack B, revealing another Queen of Hearts.
I now draw a random card from pack C and place it at the bottom of pack A.
What is the probability that the card at the top of pack C is the Ace of Spades?
![](javascript:showlimage("prob-tree.jpg"))
If you enjoyed this puzzle, check out Sunday Afternoon Maths XXVIII,
puzzles about cards, or a random puzzle.
puzzles about cards, or a random puzzle.