Sunday Afternoon Maths V
Folding tube maps
Back in 2012, I posted instructions for
folding a tetrahedron from tube maps. When tube maps are used, the sides of the tetrahedron are not quite equal. What ratio would the rectangular maps need to be in to give a regular tetrahedron?
Show answer & extension
Hide answer & extension
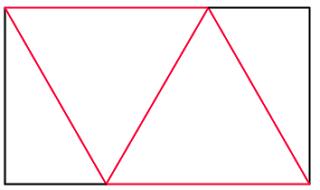
Once the map is folded, it will look like this:
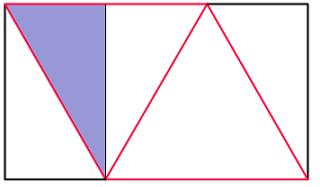
For the final tetrahedron to be regular, the red lengths must be equal. Let each red length be 2 (this will get rid of halves in the upcoming calculations). By drawing a vertical line in we can work out the width and height of the rectangle:
The width of the rectangle is 3 (one and a half red lengths). Using Pythagoras' Theorem in the blue triangle, we find that the height of the rectangle is \(\sqrt{3}\). Therefore, the ratio of the rectangle is \(\sqrt{3}:3\) or \(1:\sqrt{3}\).
Extension
If the ratio of the rectangle is \(1:a\), what is the ratio of the lengths of the sides of the tetrahedron?
x to the power of x again
Let \(y=x^{x^{x^{x^{...}}}}\) [\(x\) to the power of (\(x\) to the power of (\(x\) to the power of (\(x\) to the power of ...))) with an infinite number of \(x\)s]. What is \(\frac{dy}{dx}\)?
Show answer & extension
Hide answer & extension
\(y=x^{x^{x^{x^{...}}}}\) so \(y=x^y=e^{y\ln{x}}\).
By the chain and product rules, \(\frac{dy}{dx}=e^{y\ln{x}}(\frac{dy}{dx}\ln{x}+\frac{y}{x})\).
Rearranging, we get \(\frac{dy}{dx}=\frac{ye^{y\ln{x}}}{x(1-e^{y\ln{x}}\ln{x})}\).
This simplifies to \(\frac{dy}{dx}=\frac{x^{x^{x^{x^{...}}}}x^{x^{x^{x^{...}}}}}{x(1-x^{x^{x^{x^{...}}}}\ln{x})}\).
Extension
What would the graph of \(y=x^{x^{x^{x^{...}}}}\) look like?
Odd sums
What is \(\frac{1+3}{5+7}\)?
What is \(\frac{1+3+5}{7+9+11}\)?
What is \(\frac{1+3+5+7}{9+11+13+15}\)?
What is \(\frac{1+3+5+7+9}{11+13+15+17+19}\)?
What is \(\frac{\mathrm{sum\ of\ the\ first\ }n\mathrm{\ odd\ numbers}}{\mathrm{sum\ of\ the\ next\ }n\mathrm{\ odd\ numbers}}\)?
Show answer & extension
Hide answer & extension
They are all equal to one third.
The sum of the first \(n\) odd numbers is \(n^2\) (this can be proved by induction). This means that:
$$\frac{\mathrm{sum\ of\ the\ first\ }n\mathrm{\ odd\ numbers}}{\mathrm{sum\ of\ the\ next\ }n\mathrm{\ odd\ numbers}}=\frac{n^2}{(2n)^2-n^2}\\
=\frac{n^2}{3n^2}=\frac{1}{3}$$
Extension
What is \(\frac{\mathrm{sum\ of\ the\ first\ }n\mathrm{\ odd\ numbers}}{\mathrm{sum\ of\ the\ first\ }n\mathrm{\ even\ numbers}}\)?
Two lines
Let A and B be two straight lines such that the gradient of A is the y-intercept of B and the y-intercept of A is the gradient of B (the gradient and y-intercept of A are not the same). What are the co-ordinates of the point where the lines meet?
Show answer & extension
Hide answer & extension
Let A have the equation \(y = mx + c\). B will have the equation \(y = cx + m\).
Therefore, \(mx + c = cx + m\).
Which rearranges to \(x(m - c) = m - c.\)
So \(x = 1\).
Substituting back in, we find \(y=m+c\).
The co-ordinates of the point of intersection are \((1,m+c)\).
Extension
Let \(a\), \(b\) and \(c\) be three distinct numbers. What can you say about the points of intersection of the parabolas:
$$y = ax^2 + bx + c\mathrm{,}\\
y = bx^2 + cx + a\mathrm{,}\\
\mathrm{and\ }y = cx^2 + ax + b$$
![](javascript:showlimage("tetra1.png"))
![](javascript:showlimage("tetra2.png"))