Puzzles
4 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
| - | + | = -4 | |||
| + | + | + | |||
| - | ÷ | = -1 | |||
| - | ÷ | × | |||
| - | × | = -30 | |||
| = 0 | = 2 | = 54 |
The answer is the product of the digits in the red boxes.
The self referential crossword
Source: Alex Bellos's Monday puzzle
Fill in the following crossnumber grid so that each clue describes the solution.
For example, if some clues read "TEN DS", "ONE X" and "THREE ES" then there will be ten Ds, one X and three Es in the completed grid. The entries in the crossword include the spaces.
Make the sums
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums reading across and down are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, \(4+3\times2\) is 14, not 10.
| + | - | = 4 | |||
| + | - | × | |||
| - | × | = 27 | |||
| - | × | ÷ | |||
| × | ÷ | = 16 | |||
| = 2 | = 8 | = 6 |
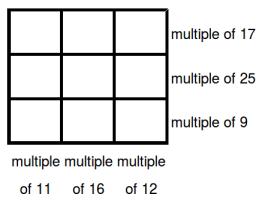
Fill in the digits
Source: Chalkdust
Can you place the digits 1 to 9 in the boxes so that the three digit numbers formed in the top, middle and bottom rows are multiples of 17, 25 and 9 (respectively); and the three digit numbers in the left, middle and right columns are multiples of 11, 16 and 12 (respectively)?