Puzzles
21 December
There are 6 two-digit numbers whose digits are all 1, 2, or 3 and whose second digit onwards
are all less than or equal to the previous digit:
- 33
- 22
- 31
- 21
- 11
- 32
How many 20-digit numbers are there whose digits are all 1, 2, or 3 and whose second digit onwards
are all less than or equal to the previous digit?
20 December
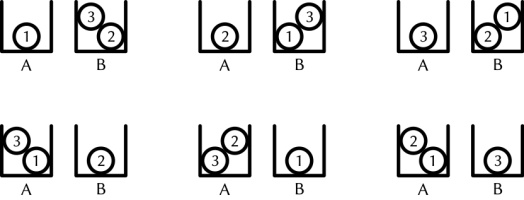
There are 6 different ways that three balls labelled 1 to 3 can be put into two boxes labelled
A and B so that no box is empty:
![](javascript:showlimage("advent2023-20dec.png"))
How many ways can five balls labelled 1 to 5 be put into four boxes labelled A to D so that
no box is empty?
19 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | – | = 7 | |||
| × | × | × | |||
| + | – | = 0 | |||
| ÷ | ÷ | ÷ | |||
| + | – | = 2 | |||
| = 4 | = 35 | = 18 |
18 December
Some numbers can be written as the product of two or more consecutive integers, for example:
$$6=2\times3$$
$$840=4\times5\times6\times7$$
What is the smallest three-digit number that can be written as the product of two or more consecutive integers?
17 December
If you expand \((a+b+c)^2\), you get \(a^2+b^2+c^2+2ab+2ac+2bc\).
This has 6 terms.
How many terms does the expansion of \((a+b+c+d+e+f)^5\) have?
16 December
Some numbers can be written as the sum of two or more consecutive positive integers, for example:
$$7=3+4$$
$$18=5+6+7$$
Some numbers (for example 4) cannot be written as the sum of two or more consecutive positive integers.
What is the smallest three-digit number that cannot be written as the sum of two or more consecutive positive integers?
15 December
The arithmetic mean of a set of \(n\) numbers is computed by adding up all the numbers, then
dividing the result by \(n\).
The geometric mean of a set of \(n\) numbers is computed by multiplying all the numbers together, then
taking the \(n\)th root of the result.
The arithmetic mean of the digits of the number 132 is \(\tfrac13(1+3+2)=2\).
The geometric mean of the digits of the number 139 is \(\sqrt[3]{1\times3\times9}\)=3.
What is the smallest three-digit number whose first digit is 4 and for which the arithmetic and geometric means of its digits are both non-zero integers?
14 December
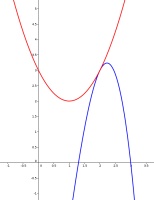
The function \(f(x)=ax+b\) (where \(a\) and \(b\) are real constants) satisfies
$$-x^3+2x^2+6x-9\leqslant f(x)\leqslant x^2-2x+3$$
whenever \(0\leqslant x\leqslant3\). What is \(f(200)\)?
![](javascript:showlimage("advent2023sol-14dec.png"))