Puzzles
24 December
There are 343 three-digit numbers whose digits are all 1, 2, 3, 4, 5, 6, or 7. What is the
mean of all these numbers?
Show answer
Hide answer
The digits 1 to 7 will each appear the same number of times as each other in each position of the number, so each digit of the mean will be the mean of the digits 1 to 7.
Therefore the mean is 444.
23 December
In a grid of squares, each square is friendly with itself and friendly with every square that is horizontally, vertically, or diagonally adjacent to it (and is not friendly with any other squares).
In a 5×5 grid, it is possible to colour 8 squares so that every square is friendly with at least two coloured squares:
It it not possible to do this by colouring fewer than 8 squares.
What is the fewest number of squares that need to be coloured in a
23×23 grid so that every square is friendly with at least two coloured squares?
22 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number that can be formed using the three digits in the red boxes.
| + | | ÷ | | = 3 |
| – | | × | | × | |
| + | | – | | = 6 |
| – | | – | | – | |
| × | | × | | = 16 |
=
1 | | =
13 | | =
16 | |
Show answer
Hide answer
| 9 | + | 3 | ÷ | 4 | = 3 |
| – | | × | | × | |
| 7 | + | 5 | – | 6 | = 6 |
| – | | – | | – | |
| 1 | × | 2 | × | 8 | = 16 |
=
1 | | =
13 | | =
16 | |
The largest number that can be formed with the red digits is 851.
21 December
Noel wants to write a different non-zero digit in each of the five boxes below so that
the products of the digits of the three-digit numbers reading across and down are the same.
What is the smallest three-digit number that Noel could write in the boxes going across?
20 December
p(x) is a polynomial with integer coefficients such that:
- p(0) > 0;
- if x is a real number,
4x – 9 < p(x) < x2 – 2x + 2.
What is p(23)?
Show answer
Hide answer
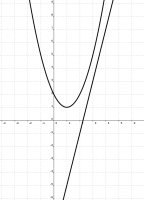
Plotting \(y = 4x - 9\) and \(y = x^2-2x+2\) gives:
As \(p(x)\) has integer coefficients, \(p(3)\) must be an integer. If you click to view a larger version of the image, you'll see that the only option for \(p(3)\) that satisfies
\(4x-9<p(x)<x^2-2x+2\) is \(p(3)=4\).
As \(p(x)>4x-9\), it must at least a polynomial of degree 1. As \(p(x)<x^2-2x+2\), it must be at most a polynomial of degree 2. Playing with coefficients, you can see that
\(p(x)\) is either \(x^2-2x+1\) or \(4x-8\). \(4x-8\) is negative when \(x=0\), so \(p(x)=x^2-2x+1\) and \(p(23)\) is 484.
19 December
There are 9 integers below 100 whose digits are all non-zero and add up to 9:
9, 18, 27, 36, 45, 54, 63, 72, and 81.
How many positive integers are there whose digits are all non-zero and add up to 9?
Show answer & extension
Hide answer & extension
All the integers whose digits are all non-zero and add up to 9 can be made by taking a list of 9 ones, and between each pair deciding whether to move on a digit or not. For example,
1111|111|11 (where | means move on) would represent the number 432; and 1|1|1111111 would represent the number 117.
There are 8 gaps between 9s, so there are 28 = 256 numbers that can be made.
Extension
Why are there not 512 positive integers whose digits are all non-zero and add up to 10?
18 December
If k = 21, then 28k ÷ (28 + k) is an integer.
What is the largest integer k such that 28k ÷ (28 + k) is an integer?
Show answer
Hide answer
If \(k\) is a multiple of 28, then let \(k=28a\) and see that:
$$\frac{28k}{28+k}=\frac{28a}{1+a}$$
This is an integer if either \(a=0\), \(a=1\), or \(1+a\) is a factor of 28. Hence the largest value of \(a\) is 27, leading to \(k\) = 756.
Similar working out can be done for the cases where the hcf of 28 and \(k\) is 14, 7, 2, or 1, and in each case a lower answer would be obtained.
17 December
The number 40 has 8 factors: 1, 2, 4, 5, 8, 10, 20, and 40.
How many factors does the number 226×5×75×112 have?
Show answer
Hide answer
The factors will all be of the form \(2^a\times5^b\times7^c\times11^d\), where
\(0\leqslant a\leqslant26\),
\(0\leqslant b\leqslant1\),
\(0\leqslant c\leqslant5\), and
\(0\leqslant d\leqslant2\). There are 27 choices for \(a\), 2 for \(b\), 6 for \(c\), and 3 for \(d\) giving a total of 27×2×6×3 = 972 factors.
![](javascript:showlimage("advent2024-23dec.png"))
![](javascript:showlimage("advent2024-21dec.png"))
![](javascript:showlimage("adv2024-ans20.png"))