Sunday Afternoon Maths XXXVIII
Posted on 2015-02-01
Products and sums of squares
Show that the product of any two numbers, each of which is the sum of two square integers, is itself the sum of two square integers.
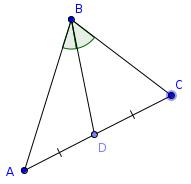
Equal side and angle
Source: Jim Noble on Twitter
In the diagram shown, the lengths \(AD = CD\) and the angles \(ABD=CBD\).
Prove that the lengths \(AB=BC\).
If you enjoyed these puzzles, check out Advent calendar 2024,
puzzles about differentiation, or a random puzzle.
puzzles about differentiation, or a random puzzle.