Sunday Afternoon Maths XXIX

(ii) Differentiating \(y=x^2\) with respect to \(x\) \(\frac{dy}{dx}=2x\). Let \(g=\frac{dy}{dx}\). By the chain rule:

So \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=\frac{1}{x}\)

(iii) By the same method, \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=\frac{2}{x}\)

(iv) \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=\frac{n-1}{x}\)

(v) \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=1\)

(vi) \(\frac{d}{dy}\left(\frac{dy}{dx}\right)=-\tan(x)\)

What is

when \(y=f(x)\)?

Let \(p_1\), \(p_2\), ..., \(p_6\) be the probabilities of getting 1 to 6 on one die and \(q_1\), ..., \(q_6\) on the other. The probability of getting a total of 2 is \(p_1q_1\) and the probabilty of getting a total of 12 is \(p_6q_6\). Therefore \(p_1q_1=p_6q_6\).

If \(p_1\geq p_6\) then \(q_1\leq q_6\) (and vice-versa) as otherwise the above equality could not hole. Therefore:

The probability of rolling a total of 7 is \(p_1q_6+p_2q_5+...+p_6q_1\). This is larger than \(p_1q_6+p_6q_1\), which is larger than (or equal to) \(p_1q_1+q_6p_6\), which is larger than \(p_1q_1\).

Therefore the probability of rolling a 7 is larger than the probability of rolling a two, so it is not possible.

Can two \(n\)-sided dice be weighted so that the probability of each of the numbers 2, 3, ..., 2\(n\) is the same?

Can a \(n\)-sided die and a \(m\)-sided die be weighted so that the probability of each of the numbers 2, 3, ..., \(n+m\) is the same?

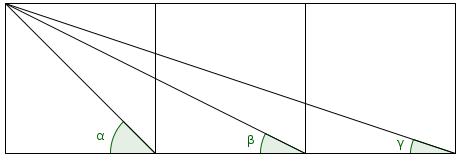
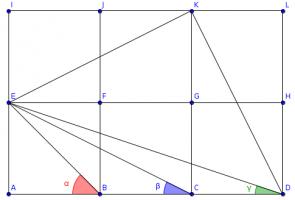
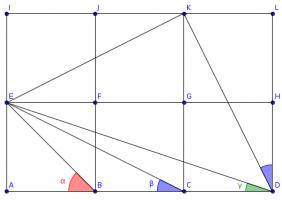
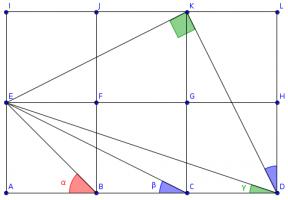
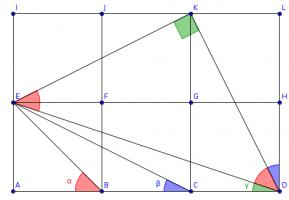
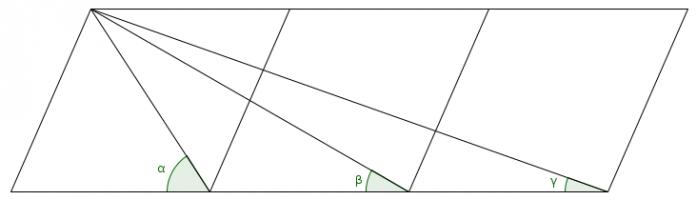
Draw three more squares and add these lines (I have coloured the angles to make equal angles clearer):

Triangles \(ACE\), \(LDK\) and \(IKE\) are congruent, so angle \(KDL\) is equal to \(\beta\).

The congruence of these triangles tells us that angles \(DKL\) and \(EKI\) add up to a right angle, so angle \(EKD\) is also a right angle.

The congruence of the triangles also tells us that \(KD\) and \(KE\) are the same length and so angle \(EDK\) is the angle in an isosceles right-angled triangle. \(\alpha\) is also the angle in an isosceles right-angled triangle, so these two angles are equal.

Therefore \(\alpha+\beta+\gamma=90^\circ\).

The diagram shows three rhombuses with diagonals drawn on and three angles labelled.

What is the value of \(\alpha+\beta+\gamma\)?