Sunday Afternoon Maths XXI
Posted on 2014-07-20
Wool circles
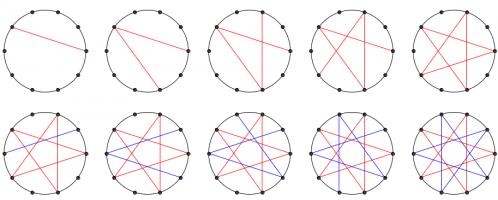
\(n\) people stand in a circle. The first person takes a ball of
wool, holds the end and passes the ball to his right, missing a
people. Each person who receives the wool holds it and passes the
ball on to their right, missing \(a\) people. Once the ball returns to
the first person, a different coloured ball of wool is given to
someone who isn't holding anything and the process is repeated. This is
done until everyone is holding wool.
For example, if \(n=10\) and \(a=3\):
![](javascript:showlimage("woolcircles.png"))
In this example, two different coloured balls of wool are needed.
In terms of \(n\) and \(a\), how many different coloured balls of
wool
are
needed?
Sum equals product
\(3\) and \(1.5\) are a special pair of numbers, as \(3+1.5=4.5\)
and
\(3\times 1.5=4.5\) so \(3+1.5=3\times 1.5\).
Given a number \(a\), can you find a number \(b\) such that
\(a+b=a\times b\)?
If you enjoyed these puzzles, check out Advent calendar 2025,
puzzles about fractions, or a random puzzle.
puzzles about fractions, or a random puzzle.