Sunday Afternoon Maths XX
Bézier curve
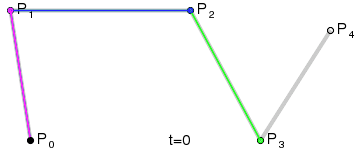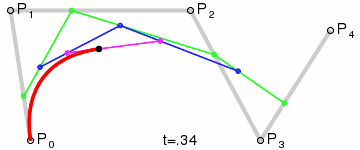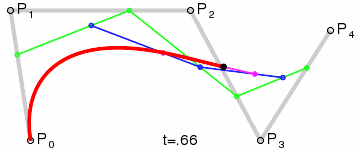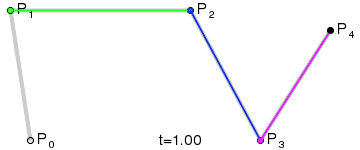
1) A set of points \(P_0\), ..., \(P_n\) are chosen (in the example \(n=4\)).
2) A set of points \(Q_0\), ..., \(Q_{n-1}\) are defined by \(Q_i=t P_{i+1}+(1-t) P_i\) (shown in green).
3) A set of points \(R_0\), ..., \(R_{n-2}\) are defined by \(R_i=t Q_{i+1}+(1-t) Q_i\) (shown in blue).
.
.
.
\(n\)) After repeating the process \(n\) times, there will be one point. The Bézier curve is the path traced by this point at \(t\) varies between 0 and 1.
What is the Cartesian equation of the curve formed when:
$$P_0=\left(0,1\right)$$
$$P_1=\left(0,0\right)$$
$$P_2=\left(1,0\right)$$
Show answer & extension
Hide answer & extension
If
$$P_0=\left(0,1\right)$$
$$P_1=\left(0,0\right)$$
$$P_2=\left(1,0\right)$$
then
$$Q_0=t\left(0,0\right)+(1-t)\left(0,1\right)=\left(0,1-t\right)$$
$$Q_1=t\left(1,0\right)+(1-t)\left(0,0\right)=\left(t,0\right)$$
and so
$$R_0=t\left(t,0\right)+(1-t)\left(0,1-t\right)=\left(t^2,(1-t)^2\right)$$
which means that
$$x=t^2$$$$y=(1-t)^2$$
or
$$y=(1-\sqrt{x})^2$$
Extension
What should \(P_0\), \(P_1\) and \(P_2\) be to get a curve with Cartesian equation
$$y=(1-\sqrt{2x})^2$$
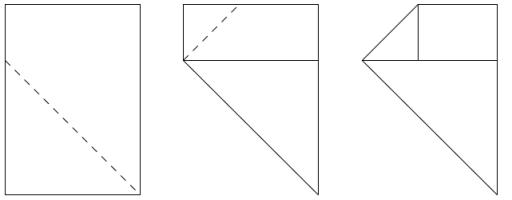
Folding A4 paper
A Piece of
A4 paper is folded as shown:
What shape is made?
Show answer & extension
Hide answer & extension
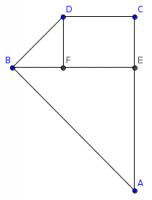
The sides of A4 paper are in the ratio \(1:\sqrt{2}\). Let the width of the paper be 1 unit. This means that the height of the paper is \(\sqrt{2}\) units.
Therefore on the diagram, \(AE=1, BE=1, AC=\sqrt{2}\). By Pythagoras' Theorem, \(AB=\sqrt{2}\), so \(AB=AC\).
\(BF=DF=\sqrt{2}-1\) so by Pythagoras' Theorem again, \(BD=2-\sqrt{2}\). \(CD=1-(\sqrt{2}-1)=2-\sqrt{2}\). Hence, \(CD=BD\) and so the shape is a kite.
Extension
Prove that for a starting rectangle with the sides in any ratio, the resulting shape is a
cyclic quadrilateral.
![](javascript:showlimage("bezier.gif"))
![](javascript:showlimage("folding-a4-paper.png"))
![](javascript:showlimage("kite.png"))