Sunday Afternoon Maths XL
The sixth cent
You toss 6 fair coins, and I toss 5 fair coins. What is the probability that you get more heads than I do?
Show answer & extension
Hide answer & extension
As You have one more coin than me, if you don't throw more heads than me, then you must throw more tails than me.
This means that the probability of you throwing more heads then me plus the probability of you throwing more tails then me is equal to one.
By symmetry, the probabilities for heads and tails must be equal and so the probability that you throw more heads is \(\frac{1}{2}\)
Extension
You toss \(n\) fair coins, and I toss \(m\) fair coins. What is the probability that you get more heads than I do?
One hundred factorial
How many zeros does \(100!\) end with?
Show answer & extension
Hide answer & extension
The number of zeros at the end of a number is the same as the number of 10s in the product that makes the number. Each of these 10s is made by multiplying 5 by 2.
There will be more even numbers than multiples of 5 in \(100!\), so the number of 5s will tell us how many zeros the number ends in.
In \(100!\), there will be 20 multiples of 5 and 4 multiples of \(5^2\). This means that \(100!\) will end in 24 zeros.
Extension
How many zeros will \(n!\) end in?
Two triangles
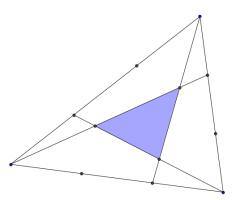
The three sides of this triangle have been split into three equal parts and three lines have been added.
What is the area of the smaller blue triangle as a fraction of the area of the original large triangle?
Show answer & extension
Hide answer & extension
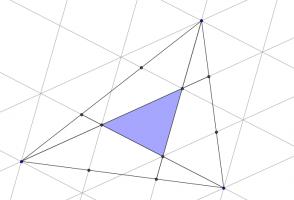
Draw on the following lines parallel to those which were added in the question.
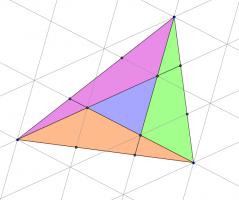
Then a grid of copies of the smaller blue triangle has been created. Now consider the three triangles which are coloured green, purple and orange in the following diagram:
Each of these traingles covers half a parallelogram made from four blue triangles. Therefore the area of each of these triangles is twice the area of the small blue triangle.
And so the blue triangle covers one seventh of the large triangle.
Extension
If the sides of the triangle were split into \(n\) pieces the the lines added, what would the area of the smaller blue triangle be as a fraction of the area of the original large triangle?
![](javascript:showlimage("two triangles.png"))
![](javascript:showlimage("two-tri-ans1.png"))
![](javascript:showlimage("two-tri-ans2.png"))