Sunday Afternoon Maths XII
Unit octagon
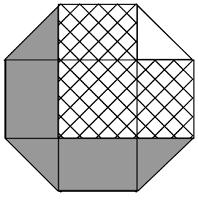
The diagram shows a regular octagon with sides of length 1. The octagon is divided into regions by four diagonals. What is the difference between the area of the hatched region and the area of the region shaded grey?
Show answer & extension
Hide answer & extension
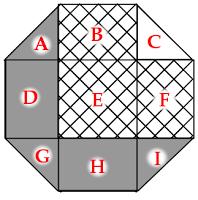
Name the regions as follows:
\(E\) is a 1×1 square. Placed together, \(A\), \(C\), \(G\) and \(I\) also make a 1×1 square. \(B\) is equal to \(H\) and \(D\) is equal to \(F\).
Therefore \(B+E+F=A+C+D+G+H+I\). Therefore the hatched region is \(C\) larger than the shaded region. The area of \(C\) (and therefore the difference) is \(\frac{1}{4}\).
Extension
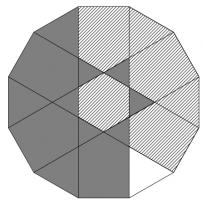
What is the difference between the shaded and the hatched regions in this dodecagon?
Largest triangle
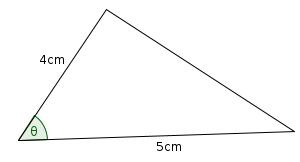
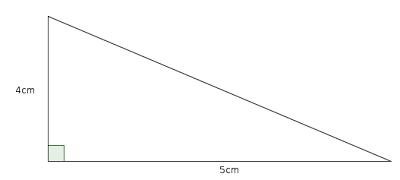
What is the largest area triangle which has one side of length 4cm and one of length 5cm?
Show answer & extension
Hide answer & extension
As our shape is a triangle, the 4cm and 5cm sides must be adjacent. Call the angle between them be \(\theta\).
The area of the triangle is \(\frac{1}{2}\times 4\times 5 \times \sin{\theta}\) or \(10\sin{\theta}\). This has a maximum value when \(\theta=90^\circ\), so the largest triangle has and area of 10cm2 and looks like:
Extension
What is the largest area triangle with a perimeter of 12cm?
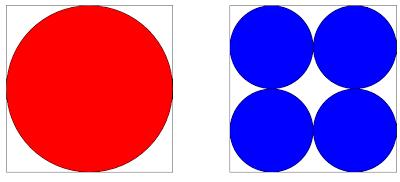
Circles
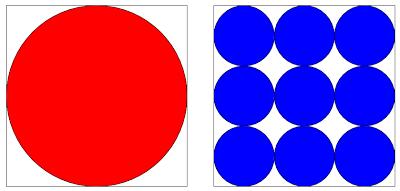
Which is largest, the red or the blue area?
Show answer & extension
Hide answer & extension
Let \(4x\) be the side length of the square. This means that the radius of the red circle is \(2x\) and the radius of a blue circle is \(x\). Therefore the area of the red circle is \(4\pi x^2\).
The area of one of the blue squares is \(\pi x^2\) so the blue area is \(4\pi x^2\). Therefore the two areas are the same.
Extension
Is the red or blue area larger?
![](javascript:showlimage("octagon.png"))
![](javascript:showlimage("octagon-a1.png"))
![](javascript:showlimage("dodecagon.png"))
![](javascript:showlimage("triangle.png"))
![](javascript:showlimage("triangle-biggest.png"))
![](javascript:showlimage("circles.png"))
![](javascript:showlimage("circles-ext.png"))