Sunday Afternoon Maths LXIV
Equal lengths
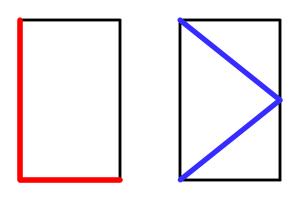
The picture below shows two copies of the same rectangle with red and blue lines. The blue line visits the midpoint of the opposite side. The lengths shown in red and blue are of equal length.
What is the ratio of the sides of the rectangle?
Show answer
Hide answer
Let \(a\) be the height of the rectangle and \(b\) be the width.
The length of the red line is \(a+b\). The length of the blue line is \(2\sqrt{a^2+\frac{b^2}4}\). These are equal so:
\begin{align}
a+b&=2\sqrt{a^2+\frac{b^2}4}\\
(a+b)^2&=4\left(a^2+\frac{b^2}{4}\right)\\
a^2+2ab+b^2&=4a^2+b^2\\
0&=3a^2-2ab\\
0&=3a-2b\\
2b&=3a
\end{align}
Therefore the ratio of the sides is 2:3.
Digitless factor
Ted thinks of a three-digit number. He removes one of its digits to make a two-digit number.
Ted notices that his three-digit number is exactly 37 times his two-digit number. What was Ted's three-digit number?
Show answer & extension
Hide answer & extension
Ted's number was 925: \(925\div25=37\).
If Ted had removed the final digit of his number, then he would be looking for a solution of \(ABC = 37\times AB\). But \(ABC\)
is between 10 and 11 times \(AB\) (it is \(10\times AB + C\)) and so cannot be 37 times \(AB\). So Ted cannot have removed the final digit.
Therefore, Ted must have removed one of the first two digits: so two- and three- digit numbers have the same final digit (\(C\)).
The final digit of the three-digit number (\(C\)) will be the final digit of \(7\times C\) (7 times the final digit of the two digit number).
This is only possible if the final digit is \(C\) is 0 or 5.
This only leaves four possible solutions—10, 15, 20 and 25—as \(30\times37>1000\). Of these only \(925=37\times25\) works.
Extension
How many three-digit numbers are there that are a multiple of one of the two-digit numbers you can make by removing a digit?
Backwards fours
If A, B, C, D and E are all unique digits, what values would work with the following equation?
$$ABCCDE\times 4 = EDCCBA$$
Show answer
Hide answer
EDCCBA is a multiple of four, so A is even. A cannot be more than 2, as otherwise EDCCBA would have more digits. So A is 2.
E must therefore be 8 or 9 (as 4 times B is less than E) and 3 or 8 (as 4 times E ends in 2). Therefore E is 8.
Carrying on like this, we find:
$$219978\times4=879912$$
![](javascript:showlimage("rectangles506.png"))