Sunday Afternoon Maths LV
Powerful quadratics
Find all real solutions to
$$(x^2-7x+11)^{(x^2-11x+30)}=1.$$
Show answer
Hide answer
If \(x^2-7x+11=1\) or \(x^2-11x+30=0\), then this is one. The solutions to these are \(x=2,5,\) and \(6\).
It could also be one if \(x^2-7x+11=-1\) and \(x^2-11x+30\) is even. This happens when \(x=3\) or \(4\).
Therefore all the solutions to this are \(x=2,3,4,5\) or \(6\).
Two tangents
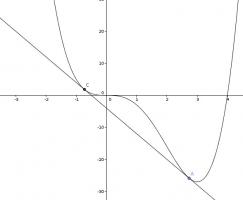
Find a line which is tangent to the curve \(y=x^4-4x^3\) at 2 points.
Show answer
Hide answer
At \(x=a\), \(y=a^4-4a^2\) and \(\frac{dy}{dx}=4a^3-12a^2\). Therefore the equation of the tangent at \(x=a\) will be \(y=(4a^3-12a^2)x+8a^3-3a^4\).
Taking this away from \(y=x^4-4x^3\) gives \(y=x^4-4x^3-(4a^3-12a^2)x-8a^3+3a^4\). We can now look at where this curve is tangent to \(y=0\) and look for a value of \(a\) that makes it tangent at two points.
If this curve is tangent to the \(x\)-axis at \(x=b\), then it will have a repeated root at \(x=b\). We know it is tangent at \(x=a\), so dividing \(x^4-4x^3-(4a^3-12a^2)x-8a^3+3a^4\) by \((x-a)\) twice gives \(x^2+(2a-4)x+3a^2-8a\). We want this to have a repeated root, hence the discriminant, \((2a-4)^2-4(3a^2-8a)\), must be 0.
Solving this gives \(a=1\pm\sqrt3\).
Therefore the equation of the line is \(y=-8x-4\).
Blackboard sums
The numbers 1 to 20 are written on a blackboard. Each turn, you may erase two numbers, \(a\) and \(b\) and write the sum \(a+b\) in their place. You continue until only one number remains.
What is the largest number you can make?
Show answer & extension
Hide answer & extension
After each turn, the total of the numbers written on the board remains the same. Therefore the sum of the numbers is always the same: 210
Extension
The numbers 1 to 20 are written on a blackboard. Each turn, you may erase two numbers, \(a\) and \(b\) and write the product \(a\times b\) in their place. You continue until only one number remains.
What is the largest number you can make?