Puzzles
Square deal
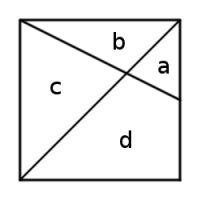
This unit square is divided into four regions by a diagonal and a line that connects a vertex to the midpoint of an opposite side. What are the areas of the four regions?
Show answer & extension
Hide answer & extension
The square is unit, so \(a+b+c+d=1\). By the definitions of the lines, \(a+d=\frac{1}{2}\) and \(a+b=\frac{1}{4}\).
\(a\) and \(c\) are similar triangles. The vertical side of \(c\) is twice that of \(a\) so \(c=4a\).
Therefore we have the system of simultaneous equations:
$$a+b+c+d=1\\a+d=\frac{1}{2}\\a+b=\frac{1}{4}\\c=4a$$
These can be solved to find:
$$a=\frac{1}{12}\\b=\frac{1}{6}\\c=\frac{1}{3}\\d=\frac{5}{12}\\$$
Extension
What would be the areas if the lines were a diagonal and another line which divides the sides in the ratio \(x:y\)?
![](javascript:showlimage("square-deal.png"))