Puzzles
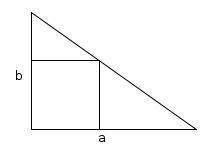
Square in a triangle
Source: Maths Jam
A right-angled triangle has short sides of length \(a\) and \(b\). A square is drawn in the triangle so that two sides lie on the sides of the triangle and a corner lies on the hypotenuse.
![](javascript:showlimage("sq-in-tri.png"))
What is the length of a side of the square?
If you enjoyed this puzzle, check out Sunday Afternoon Maths XXX,
puzzles about 2d shapes, or a random puzzle.
puzzles about 2d shapes, or a random puzzle.