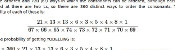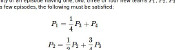Blog
2014-04-11
As well as letters games, the contestants on Countdown also take part in numbers games. Six numbers are chosen from the large numbers (25,50,75,100) and small numbers (1-10, two cards for each number) and a total between 101 and 999 (inclusive) is chosen by CECIL. The contestants then use the six numbers, with multiplication, addition, subtraction and division, to get as close to the target number as possible.
The best way to win the numbers game is to get the target exactly. This got me wondering: is there a combination of numbers which allows you to get every total between 101 and 999? And which combination of large and small numbers should be picked to give the highest chance of being able to get the target?
To work this out, I got my computer to go through every possible combination of numbers, trying every combination of operations. (I had to leave this running overnight as there are a lot of combinations!)
Getting every total
There are 61 combinations of numbers which allow every total to be obtained. These include the following (click to see how each total can be made):
- 5 6 8 9 10 100
- 5 6 7 8 10 100
- 4 6 7 8 9 100
- 3 6 7 8 10 100
- 3 5 7 8 9 100
- 2 5 6 8 9 100
- 2 6 7 8 9 100
- 5 6 8 9 75 100
- 3 6 8 10 75 100
- 2 6 9 10 75 100
By contrast, the following combination allows no totals between 101 and 999 to be reached:
- 1 1 2 2 3 3
The number of attainable targets for each set of numbers can be found here.
Probability of being able to reach the target
Some combinations of numbers are more likely than others. For example, 1 2 25 50 75 100 is four times as likely as 1 1 25 50 75 100, as (ignoring re-orderings) in the first combination, there are two choices for the 1 tile and 2 tile, but in the second combination there is only one choice for each 1 tile. Different ordering of tiles can be ignored as each combination with the same number of large tiles will have the same number of orderings.
By taking into account the relative probability of each combination, the following probabilities can be found:
| Number of large numbers | Probability of being able to reach target |
| 0 | 0.964463439 |
| 1 | 0.983830962 |
| 2 | 0.993277819 |
| 3 | 0.985770510 |
| 4 | 0.859709475 |
So, in order to maximise the probability of being able to reach the target, two large numbers should be chosen.
However, as this will mean that your opponent will also be able to reach the target, a better strategy might be to pick no large numbers or four large numbers and get closer to the target than your opponent, especially if you have practised pulling off answers like this.
Edit: Numbers corrected.
Edit: The code used to calculate the numbers in this post can now be found here.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2016-07-20
@Francis Galiegue: I've pushed a version of the code to https://github.com/mscroggs/countdown-...Matthew
@Francis Galiegue: Sadly, I lost the code I used when I had laptop problems. However, I can remember what it did, so I shall recreate it and put it on GitHub.
Matthew
If you could, I'd love to have the code you used to do this exhaustive search?
I'm a fan of the game myself (but then I'm French, so to me it's the original, "Des chiffres et des lettres"), but for the numbers game, this is pretty much irrelevant to the language and country :)
I'm a fan of the game myself (but then I'm French, so to me it's the original, "Des chiffres et des lettres"), but for the numbers game, this is pretty much irrelevant to the language and country :)
Francis Galiegue
Add a Comment
2014-04-06
On Countdown, contestants have to make words from nine letters. The contestants take turns to choose how many vowels and consonants they would like. This got me wondering which was the best combination to pick in order to get a nine letter word.
Assuming the letters in countdown are still distributed like this, the probability of getting combinations of letters can be calculated. As the probability throughout the game is dependent on which letters have been picked, I have worked out the probability of getting a nine letter word on the first letters game.
The probability of YODELLING
YODELLING has three vowels and six consonants. There are 6 (3!) ways in which the vowels could be ordered and 720 (6!) ways in which the consonants can be ordered, although each is repeated at there are two Ls, so there are 360 distinct ways to order the consonants. The probability of each of these is:
$$\frac{21\times 13\times 13\times 6\times 3\times 5\times 4\times 8\times 1}{67\times 66\times 65\times 74\times 73\times 72\times 71\times 70\times 69}$$
So the probability of getting YODELLING is:
$$\frac{6\times 360\times 21\times 13\times 13\times 6\times 3\times 5\times 4\times 8\times 1}{67\times 66\times 65\times 74\times 73\times 72\times 71\times 70\times 69} = 0.000000575874154$$
The probability of any nine letter word
I got my computer to find the probability of every nine letter word and found the following probabilities:
| Consonants | Vowels | Probability of nine letter word |
| 0 | 9 | 0 |
| 1 | 8 | 0 |
| 2 | 7 | 0 |
| 3 | 6 | 0.000546 |
| 4 | 5 | 0.019724 |
| 5 | 4 | 0.076895 |
| 6 | 3 | 0.051417 |
| 7 | 2 | 0.005662 |
| 8 | 1 | 0.000033 |
| 9 | 0 | 0 |
So the best way to get a nine letter word in the first letters game is to pick five consonants and four vowels.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2013-12-15
Last week, I was watching Pointless and began wondering how likely it is that a show features four new teams.
On the show, teams are given two chances to get to the final—if they are knocked out before the final round on their first appearance, then they return the following episode. In all the following, I assumed that there was an equal chance of all teams winning.
If there are four new teams on a episode, then one of these will win and not return and the other three will return. Therefore the next episode will have one new team (with probability 1). If there are three new teams on an episode: one of the new teams could win, meaning two teams return and two new teams on the next episode (with probability 3/4); or the returning team could win, meaning that there would only one new team on the next episode. These probabilities, and those for other numbers of teams are shown in the table below:
| No of new teams today | |||||
Noof new teams tomorrow
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 0 | \(\frac{1}{4}\) | 1 | |
| 2 | 0 | \(\frac{1}{2}\) | \(\frac{3}{4}\) | 0 | |
| 3 | \(\frac{3}{4}\) | \(\frac{1}{2}\) | 0 | 0 | |
| 4 | \(\frac{1}{4}\) | 0 | 0 | 0 | |
Call the probability of an episode having one, two, three or four new teams \(P_1\), \(P_2\), \(P_3\) and \(P_4\) respectively. After a few episodes, the following must be satisfied:
$$P_1=\frac{1}{4}P_3+P_4$$
$$P_2=\frac{1}{2}P_2+\frac{3}{4}P_3$$
$$P_3=\frac{3}{4}P_3+\frac{1}{2}P_4$$
$$P_4=\frac{1}{4}P_1$$
And the total probability must be one:
$$P_1+P_2+P_3+P_4=1$$
These simultaneous equations can be solved to find that:
$$P_1=\frac{4}{35}$$
$$P_2=\frac{18}{35}$$
$$P_3=\frac{12}{35}$$
$$P_4=\frac{1}{35}$$
So the probability that all the teams on an episode of Pointless are new is one in 35, meaning that once in every 35 episodes we should expect to see all new teams.
Edit: This blog answered the same question in a slightly different way before I got here.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2013-07-24
A news story on the BBC Website caught my eye this morning. It reported the following "uncanny coincidence" between a Northern Irish baby and a Royal baby:
But both new mothers share the name Catherine, the same birthday - 9 January - and now their sons also share the same birth date.

I decided to work out just how uncanny this is.
The Office for National Statistics states that 729,674 babies are born every year in the UK. This works out at 1,999 babies born each day, assuming that births are uniformly distributed, so there will be approximately 1,998 babies who share Price Nameless's birthday.
So, what is the chance of the mother of one of these babies having the same birthday as Princess Kate? To work this out I used a method similar to that which is used in the birthday "paradox", which tells us that in a group of 23 people there is a more than 50% chance of two people sharing a birthday, but that's another story.
First, we look at one of our 1,998 mothers. The chance that she shares Princess Kate's birthday is 1/365 (ignoring leap days). The chance that she does not share Princess Kate's Birthday is 364/365.
Next we work out the probability that none of our 1,998 mothers shares Princess Kate's birthday. As our mothers' birthdays are independent we can multiply the probabilities together to do this (this is why we are looking at the probability of not sharing a birthday instead of sharing a birthday). Our probability therefore is \(\left(\frac{364}{365}\right)^{1998} = 0.00416314317\).
Back to the original question, we wanted to know the probability that one of our mothers shares Princess Kate's birthday. To calculate this we do take 0.00416314317 away from 1. This gives 0.99583685682 or 99.6%.
There is a 99.6% chance that there is a resident of the UK who shares the same birthday as Princess Kate and had a child on the same day.
Uncanny.
But let's be fair. The mother in our story is also called Kate. So what are the chances of that? In fact, the same method can be followed, working with the probability of having neither the same birthday or name as Princess Kate.
I think it is safe to assume that this would still be considered news-worthy if our non-princess was called Katie, Cate, Cathryn, Katie-Rose or any other name which is commonly shortened to Kate, so I included a number of variations and used this fantastic tool to find the probability of a mother being called Kate. The data only goes back to 1996, but as the name is dropping in popularity, we can assume that before 1996 at least 1.5% of babies were called Kate. Disregarding males, we can estimate that 3% of mothers are called Kate.
If anyone would like the details of the rest of the calculation, please comment on this post and I will include it here. For anyone who trusts me and isn't curious, I eventually found that the probability of none of our 1,998 mothers share the same name and birthday as Princess Kate is 0.84855028964. So the probability of another Kate having a child on the same day and sharing Princess Kate's birthday is 0.15144971035 or 15.1%. Just over one in seven.
So this is as uncanny as anything else which has a probability of one in seven, such as the Royal baby being born on a Monday (uncanny!).
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment