Blog
2023-04-12
If, like me, you grew up in the 90s, then one of your earliest experiences of programming was
probably using Logo. In Logo, you use various commands to move a "turtle" around the screen. As the turtle moves,
it can draw lines. I have a very strong memory from early secondary school of spending a few maths
lessons in the computer room writing Logo programs to draw isometric houses.
If you read this blog regularly, you'll probably have noticed that I'm a fan of the game
Asteroids. Over the last few weeks, I've been working on Logo Asteroids,
a version of Asteroids where you control your spaceship using Logo commands. You can play this game
at mscroggs.co.uk/logo.
If you've not used Logo before, or if it's been so long since you have that you've forgotten the commands,
this blog post will guide you through how to get started. If you're confident in your Logo skills,
you might still want to scroll to the end of this post, where I share some custom Logo commands that you
might find helpful.
The game's source code is available on Github;
you can also use the GitHub issue tracker to report bugs and make feature requests.
Moving the turtle
If you're starting out in Logo, the first thing you'll want to do is move the turtle.
You can move it forwards or backwards using the commands fd or
bk followed by a number of pixels:
Logo
fd 100
bk 75
To change the direction in which the turtle is facing, you can use the command rt (right)
or lt (left) followed by an angle in degrees:
Logo
rt 90
lt 45
You can also chain together multiple commands on a single line like this:
Logo
fd 100 rt 90 fd 100 lt 90
By default, a line is drawn whenever the turtle moves forward or backwards. You can stop lines from being
drawn by running the command pu (pen up). To start drawing again, run
pd (pen down). If you want to make the game needlessly harder for yourself, you can use the command ht (hide turtle). To make the game easier again, run st (show turtle).
In a normal Logo program, the lines that you draw will stay there until you clear the screen (cs). In Logo Asteroids, the lines will only be visible for a limited amount
of time, and the asteroids will bounce off them while they are visible. To prevent too many lines from being drawn too quickly,
the turtle can move a maximum of 1000 pixels in a single command (or chain of commands).
Special commands for Logo Asteroids
As well as the Logo commands, there are some commands I have included that are specific to Logo
Asteroids. These are:
Logo
start
fire
help
The command start will start the game. You'll need to run this before you can run any other commands. You'll also need to run it to start the game again if you
run out of lives.
The command fire will fire at the asteroids. This command can be run
a maximum of 10 times by a single chain of commands.
The command help will show details of all the available commands below the game.
Defining your own subroutines
If you write some Logo commands that you want to use lots of times, use can use the to command to define a subroutine.
For example, the following code defined a command called square that will draw a square of side length 50.
Logo
to square fd 50 rt 90 fd 50 rt 90 fd 50 rt 90 fd 50 rt 90 end
The subroutine can then be used by running:
Logo
square
The square subroutine can be simplified by using the repeat command:
Logo
to square repeat 4 [fd 50 rt 90] end
... or it could be made to take a side length as input:
Logo
to square :side repeat 4 [fd :side rt 90] end
This updated version of the square subroutine can then be used by running:
Logo
square 50
square 100
square 125
Helpful subroutines for Logo Asteroids
To help you get going with Logo Asteroids, I've written a few subroutines that you might find helful. See if you
can work out what they do before running them.
Logo
to burst repeat 10 [fire rt 36] end
to protect pu fd 30 pd rt 135 repeat 4 [fd 30 * sqrt 2 rt 90] lt 135 pu bk 30 pd end
to multifire rt 10 repeat 10 [fire lt 2] rt 10 end
If you write your own helpful subroutine, share it in the comments below. You can put <logo> and </logo> HTML tags around your subroutine to make it display more nicely in your comment.
To end this blog post, here's one final subroutine for you to try out:
Logo
to house pu setxy 400 225 seth 0 pd lt 30 fd 40 lt 60 fd 40 lt 120 fd 40 lt 60 fd 40 rt 120 fd 50 rt 60 fd 40 rt 120 fd 50 setxy 400 + 20 * cos 30 155 rt 180 fd 50 setxy 400 - 50 * cos 30 160 pu setxy 400 + 20 * cos 30 155 pd setxy 400 + 40 * cos 30 165 pu setxy 400 225 lt 60 pd fd 50 rt 60 fd 50 rt 120 fd 50 pu rt 60 fd 20 pd lt 120 fd 20 rt 120 fd 10 rt 60 fd 20 rt 60 fd 50 pu rt 60 fd 10 pd rt 120 fd 50 ht end
×5 ×5 ×3 ×3 ×5(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2023-04-13
Very cool! Here's a combination of your "burst" and "protect" subroutines:
to f pu sety 195 setx 390 pd repeat 10 [fire fd 20 rt 36] pu home end
Aaron
×3 ×3 ×4 ×4 ×4 I didn't include this one in the blog post, but here's a bonus fun command:
×4 ×4 ×4 ×4 ×5
to randwalk repeat 100 [rt random 360 fd 10] end
Matthew
×4 ×4 ×4 ×4 ×5 Add a Comment
2023-03-14
A circle of radius \(r\) on a piece of paper can be thought of as a line through all the points on the paper that are a distance \(r\) from the centre of the circle.
The length of this line (ie the circumference) is \(2\pi r\).
Due to the curvature of the Earth, the line through all the points that are a distance \(r\) from where you are currently standing will be less than \(2\pi r\) (although you might
not notice the difference unless \(r\) is very big). The type of curvature that a sphere has is often called positive curvature.
It is also possible to create surfaces that have negative curvature; or surfaces where the length of the line through all the points that are a distance \(r\) from a point is more than \(2\pi r\).
These surfaces are called hyperbolic surfaces.
Hyperbolic surfaces
The most readily available example of a hyperbolic surface is a Pringle: Pringles are curved upwards in one direction, and curved downwards in the other direction.
![](javascript:showlimage("pringles.jpg"))
Pringles
It's not immediately obvious what a larger hyperbolic surface would look like, but you can easily make one if you know how to crochet: simply increase the number of stitches at a
constant rate.
![](javascript:showlimage("crochet-hyper.jpg"))
A hyperolic surface that I crocheted
If it was possible to continue crocheting forever, you'd get an unbounded hyperbolic surface: the hyperbolic plane.
Over the last few weeks, I've been working on adding hyperbolic levels to Mathsteroids, the asteroids-inspired game that I started making levels for in 2018.
There are quite a few different ways to represent the hyperbolic plane in 2D. In this blog post we'll take a look at some of these; I encourage you to play the Mathsteroids level for each one as you
read so that you can get a feeling for their behaviour.
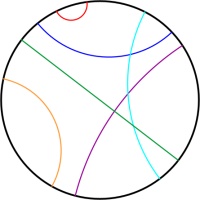
Poincaré disk
The Poincaré disk represents the hyperbolic plane as the interior of a circle. As objects move away from the centre of the circle, they appear smaller and smaller; and the circumference of
the circle is infinitely far from the centre of the circle. Straight lines on the hyperbolic plane appear on the Poincaré disk as either circles that meet the edge of the disk at right angles,
or straight lines through the centre of the circle.
![](javascript:showlimage("hyper-poincare-lines.png"))
Some examples of straight lines represented on the Poincaré disk
One of the nicest properties of the Poincaré disk is that it correctly represents angles: If you measure the angle between to intersecting straight lines represented on the disk, then the value
you measure will be the same as the angles between the two lines in the actual hyperbolic plane.
This representation can be used to demonstrate some interesting properties of the hyperbolic plane.
In normal two dimensional space, if you are given a line and a point then there is exactly one line that goes through the point and is parallel to the first line.
But in hyperbolic space, there are many such parallel lines.
![](javascript:showlimage("hyper-poincare-parallel.png"))
Parallel lines on the Poincaré disk: all of the red lines are parallel to the blue line
In Mathsteroids, there are two levels based on the Poincaré disk. The first level is bounded: you can only fly so far from the centre of the circle before
you hit the edge of the level and bounce back. (This prevents you from getting lost in the part of the disk where you would appear very very small.)
The second level is unbounded. In this level, you can fly as far as you like in any direction, but the point which is at the centre of the
disk will change when you go too far to prevent the ship from getting to small.
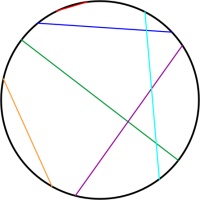
Beltrami–Klein disk
Simlar to the Poincaré disk, the Beltrami–Klein disk represents the hyperbolic plane using the interior of a circle, with the edge of the circle infinitely far away. Straight lines
in hyperbolic space will appear as straight lines in the Beltrami–Klein disk. The Beltrami–Klein disk is closely related to the Poincaré disk: the same line represented on both disks
will have its endpoints at the same points on the circle (although these endpoints are arguably not part of the line as they are on the circle that is infinitely far away).
![](javascript:showlimage("hyper-bk-lines.png"))
Some examples of straight lines represented on the Beltrami–Klein disk
Unlike in the Poincaré disk, angles are not correctly represented in the Beltrami–Klein disk. It can however be a very useful representation as straight lines appearing as straight lines
is a helpful feature.
Again, there are two Mathsteroids levels based on the Beltrami–Klein disk: a bounded level and an unbounded level.
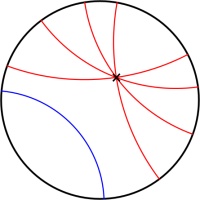
Poincaré half-plane
The Poincaré half-plane represents the hyperbolic plane using the half-plane above the \(x\)-axis. Straight lines in hyperbolic space are represented by either vertical
straight lines or semicircles with their endpoints on the \(x\)-axis.
![](javascript:showlimage("hyper-php-lines.png"))
Some examples of straight lines represented on the Poincaré half-plane
Like the Poincaré disk, the Poincaré half-plane correctly represents the angles between lines.
There is one Mathsteroids level based on the Poincaré half-plane: this level is bounded so you can only travel so far away from where you start.
Band
The band representation represents the hyperbolic plane as the strip between two horizontal lines. The strip extends forever to the left and right.
Straight lines on the band come in a variety of shapes.
![](javascript:showlimage("hyper-band-lines.png"))
Some examples of straight lines represented on the band
There is one Mathsteroids level based on the band representation: the bounded level.
Hyperboloid and Gans plane
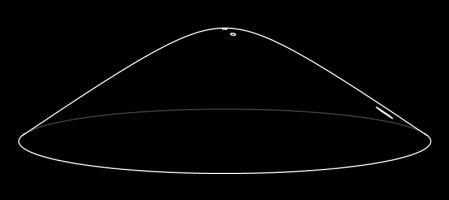
The hyperbolic plane can be represented on the surface of a hyperboloid. A hyperboloid is the shape you get if you rotate and hyperbola (a curve shaped like \(y=1/x\).)
![](javascript:showlimage("hyperbola.png"))
A hyperbola
![](javascript:showlimage("hyperboloid.png"))
A hyperboloid
Straight lines on this representation are the intersections of the hyperboloid with flat planes that go through the origin.
You can see what these straight lines look like by playing the (bounded) Mathsteroids level based on the hyperboloid.
The Gans plane is simply the hyperboloid viewed from above. There is a (bounded) Mathsteroids level based on the Gans plane.
×3 ×3 ×3 ×3 ×3(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2022-02-26
Surprisingly often, people ask me how they can build their own copy of MENACE. If you've been thinking that you'd love your own matchbox-powered machine learning computer but haven't got round to asking me about it yet, then this blog post is just what you're looking for.
Matchboxes
Before building MENACE, you'll need to get hold of 304 matchboxes (plus a few spares in case one gets lost or falls apart). I used these craft matchboxes: they don't have the best build quality, but they're good enough.
304 positions
The positions you need to glue onto the front of the matchboxes can be downloaded from this GitHub repository (first move boxes, third move boxes, fifth move boxes, seventh move boxes). These are sized to fit on matchboxes that have 15mm by 35mm fronts.
I printed each pdf on differently coloured paper to make it easier to sort the matchboxes after getting them out of their box.
If you get differently sized matchboxes, the code used the generate the PDFs is in the same GitHub repository (you'll need to modify these lines). Alternatively, feel free to drop me an email and I will happily adjust the sizes for you and send you the updated PDFs.
Glue
I used PVA glue to stick the positions onto the matchboxes. The printable PDFs have extra tabs of paper above and below the postions that can be glued in to the bottom and inside of the matchbox tray to hold it more securely.
Gluing the positions onto the matchboxes was the most time consuming part of building my copy of MENACE, largely due to having to wait for the glue to dry on a set of matchboxes before I had space for the next batch of them to dry.
Beads
Once you've glued pictures of noughts and crosses positions to 304 matchboxes, you'll need to put coloured beads into each matchbox. For this, I used a large tub of Hama beads (that tub contained orders of magnitude more beads than I needed).
A nice side effect of using Hama beads is that they're designed to be ironed together so making a key to show which colour corresponds to each position is very easy.
I typically start the boxes off with 8 beads of each colour in the first move box, 4 of each colour in the third move boxes, 2 of each in the fifth move boxes, and one of each in the seventh move boxes.
Once you've filled all your matchboxes with the correct number of beads, you're ready to play yout first game against MENACE. I'd love to hear how you get on.
And once you're bored of playing noughts and crosses against your matchboxes, why not build a machine that learns to play Hexapawn, Connect 4, Chess or Go? Or one that plays Nim?
Edit: Added link to the printable pdfs of the positions needed for Hexapawn, made by Dan Whitman.
×9 ×6 ×5 ×6 ×7(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Interesting.
Could try a same kind of thing using playing card deck(s)? A(=1)-2-3 4-5-6 7-8-9 maybe 3 decks with different colours on their backs.×3 ×3 ×3 ×3 ×2
Could try a same kind of thing using playing card deck(s)? A(=1)-2-3 4-5-6 7-8-9 maybe 3 decks with different colours on their backs.
Willem
×3 ×3 ×3 ×3 ×2 I also read the Martin Gardner article way back when and had two matchbox machines (actually with envelopes instead of matchboxes) play Nim against each other. I don't remember all the details now, except that it got to the point where one would make the first move and the other would immediately resign.×5 ×2 ×2 ×2 ×2
Tim Lewis
×5 ×2 ×2 ×2 ×2 I made a matchbox machine that learns to play 3x3 Nim almost 50 years ago. I still have it. (Based on Martin Gardner's article)
×7 ×4 ×2 ×2 ×3
Tony
×7 ×4 ×2 ×2 ×3 Add a Comment
2019-12-27
In tonight's Royal Institution Christmas lecture,
Hannah Fry and Matt Parker demonstrated how machine learning works using MENACE.
The copy of MENACE that appeared in the lecture was build and trained by me. During the training, I logged all the moved made by MENACE and the humans playing against them, and using this data I have
created some visualisations of the machine's learning.
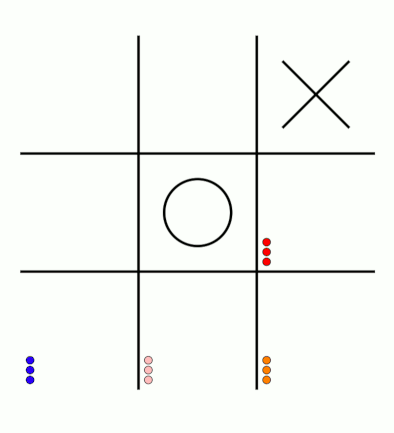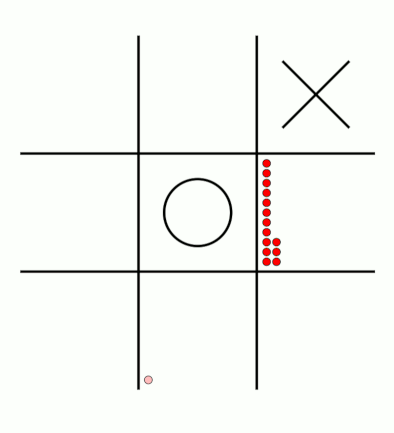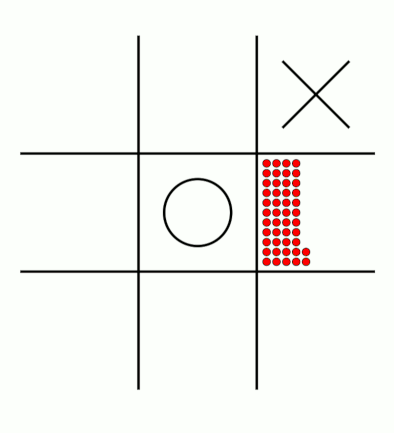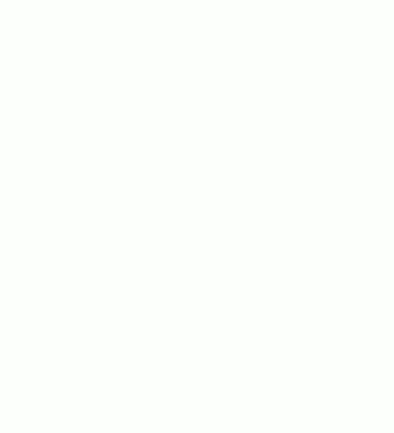
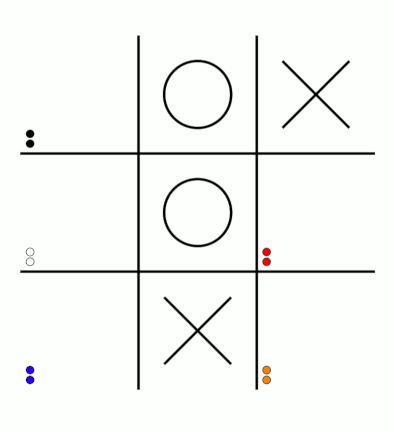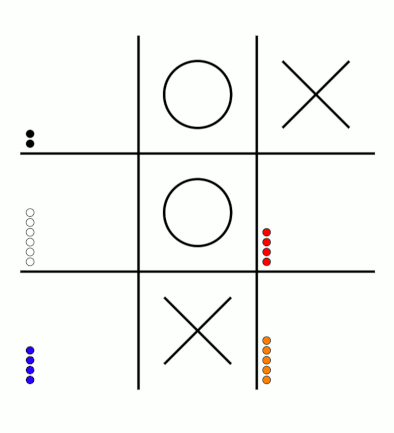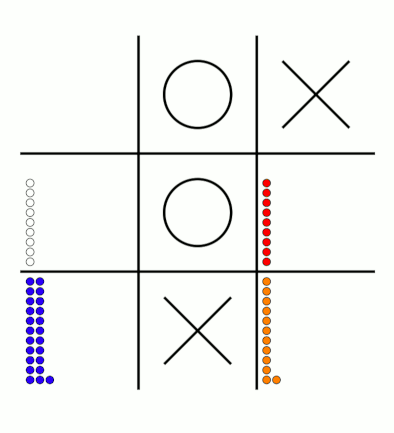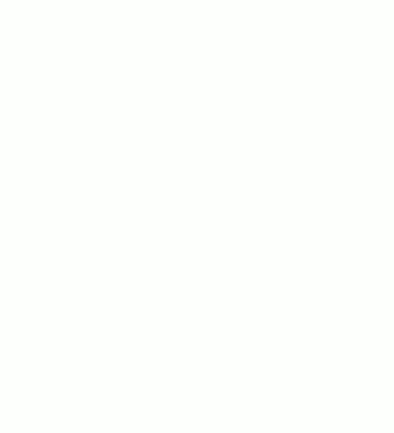
First up, here's a visualisation of the likelihood of MENACE choosing different moves as they play games. The thickness of each arrow represented the number of beads in the box corresponding to that move,
so thicker arrows represent more likely moves.
The likelihood that MENACE will play each move.
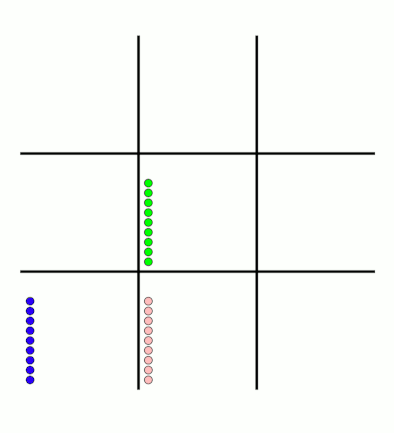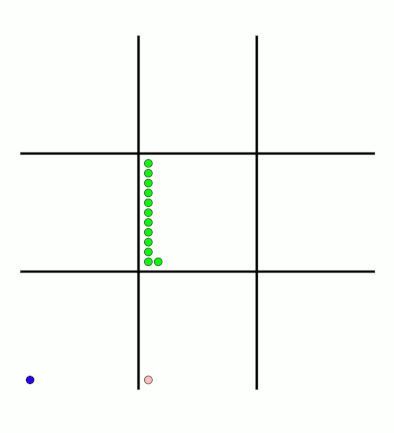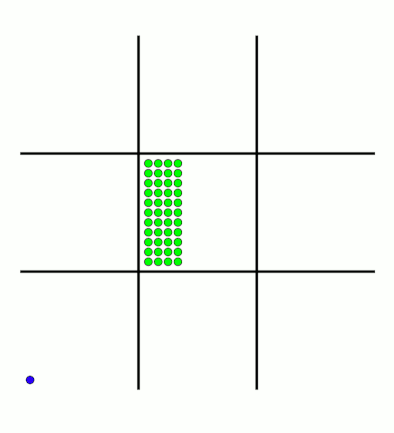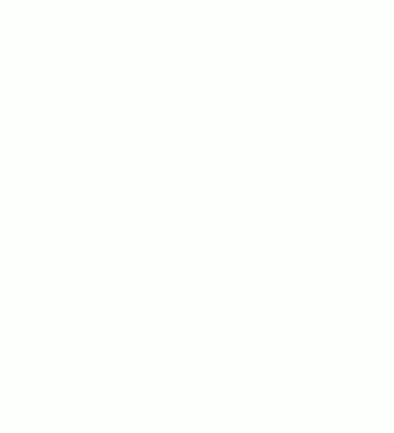
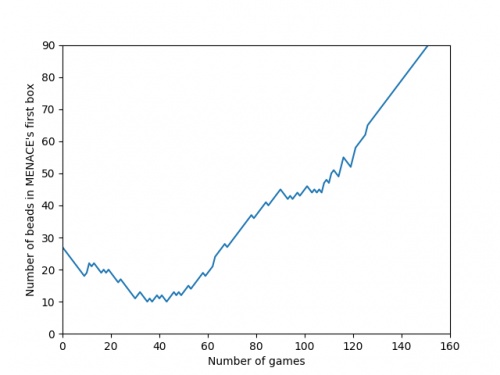
There's an awful lot of arrows in this diagram, so it's clearer if we just visualise a few boxes. This animation shows how the number of beads in the first box changes over time.
![](javascript:showlimage("MENACE_pos0.gif"))
The beads in the first box.
You can see that MENACE learnt that they should always play in the centre first, an ends up with a large number of green beads and almost none of the other colours. The following
animations show the number of beads changing in some other boxes.
![](javascript:showlimage("MENACE_pos4455.gif"))
MENACE learns that the top left is a good move.
![](javascript:showlimage("MENACE_pos13203.gif"))
MENACE learns that the middle right is a good move.
![](javascript:showlimage("MENACE_pos15396.gif"))
MENACE is very likely to draw from this position so learns that almost all the possible moves are good moves.
The numbers in these change less often, as they are not used in every game: they are only used when the game reached the positions shown on the boxes.
We can visualise MENACE's learning progress by plotting how the number of beads in the first box changes over time.
![](javascript:showlimage("MENACE_progress.png"))
The number of beads in MENACE's first box.
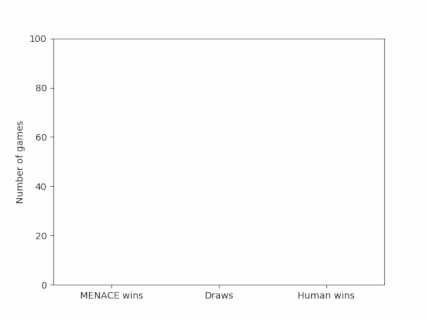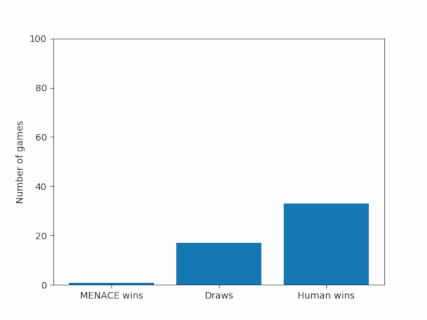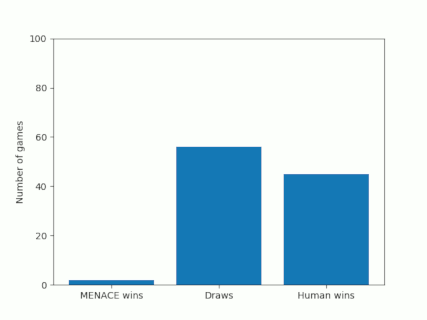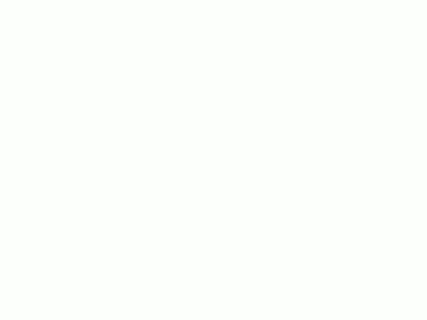
Alternatively, we could plot how the number of wins, loses and draws changes over time or view this as an animated bar chart.
![](javascript:showlimage("MENACE_progress_wld.png"))
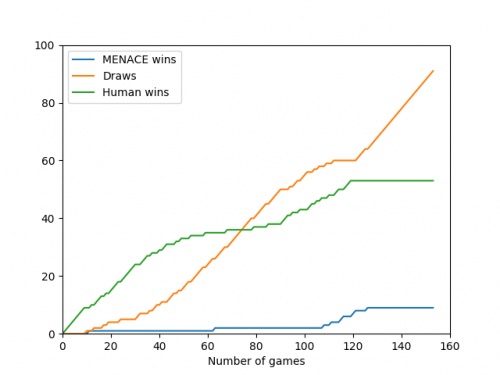
The number of games MENACE wins, loses and draws.
![](javascript:showlimage("MENACE_progress_wldbar.gif"))
The number of games MENACE has won, lost and drawn.
If you have any ideas for other interesting ways to present this data, let me know in the comments below.
×1 (Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@(anonymous): Have you been refreshing the page? Every time you refresh it resets MENACE to before it has learnt anything.
It takes around 80 games for MENACE to learn against the perfect AI. So it could be you've not left it playing for long enough? (Try turning the speed up to watch MENACE get better.)
It takes around 80 games for MENACE to learn against the perfect AI. So it could be you've not left it playing for long enough? (Try turning the speed up to watch MENACE get better.)
Matthew
I have played around menace a bit and frankly it doesnt seem to be learning i occasionally play with it and it draws but againt the perfect ai you dont see as many draws, the perfect ai wins alot more
(anonymous)
@Colin: You can set MENACE playing against MENACE2 (MENACE that plays second) on the interactive MENACE. MENACE2's starting numbers of beads and incentives may need some tweaking to give it a chance though; I've been meaning to look into this in more detail at some point...
Matthew
Idle pondering (and something you may have covered elsewhere): what's the evolution as MENACE plays against itself? (Assuming MENACE can play both sides.)
Colin
Add a Comment
2018-12-16
By now, you've probably noticed that I like teaching matchboxes to play noughts and crosses.
Thanks to comments on Hacker News, I discovered that I'm not the only one:
MENACE has appeared in, or inspired, a few works of fiction.
The Adolescence of P-1
![](javascript:showlimage("p1book.jpg"))
The Adolescence of P-1 by Thomas J Ryan [1] is the story of Gregory Burgess, a computer programmer who writes a computer program that becomes sentient.
P-1, the program in question, then gets a bit murdery as it tries to prevent humans from deactivating it.
The first hint of MENACE in this book comes early on, in chapter 2, when Gregory's friend Mike says to him:
"Because I'm a veritable fount of information. From me you could learn such wonders as the gestation period of an elephant or how to teach a matchbox to win at tic-tac-toe."Taken from The Adolescence of P-1 by Thomas J Ryan [1], page 27
A few years later, in chapter 4, Gregory is talking to Mike again. Gregory asks:
"... How do you teach a matchbox to play tic-tac toe?""What?""You heard me. I remember you once said you could teach a matchbox. How?""Jesus Christ! Let me think . . . Yeah . . . I remember now. That was an article in Scientific American quite a few years ago. It was a couple of years old when I mentioned it to you, I think.""How does it work?""Pretty good. Same principal of reward and punishment you use to teach a dog tricks, as I remember. Actually, you get several matchboxes. One for each possible move you might make in a game of tic-tac-toe. You label them appropriately, then you put an equal number of two different coloured beads in each box. The beads correspond to each yes/no decision you can make in a game. When a situation is reached, you grab the box for the move, shake it up, and grab a bead out of it. The bead indicates the move. You make a record of that box and color, and then make the opposing move yourself. You move against the boxes. If the boxes lose the game, you subtract a bead of the color you used from each of the boxes you used. If they win, you add a bead of the appropriate color to the boxes you used. The boxes lose quite a few games, theoretically, and after the bad moves start getting eliminated or statistically reduced to inoperative levels, they start to win. Then they never lose. Something like that. Check Scientific American about four years ago. How is this going to help you?"Taken from The Adolescence of P-1 by Thomas J Ryan [1], pages 41-42
The article in Scientific American that they're talking about is obviously A matchbox game learning-machine by Martin Gardner [2].
Mike, unfortunately, hasn't quite remembered perfectly how MENACE works: rather than having two colours in each box for yes and no, each box actually has a different colour for each possible move that could be made next.
But to be fair to Mike, he read the article around two years before this conversation so this error is forgivable.
In any case, this error didn't hold Gregory back, as he quickly proceeded to write a program, called P-1 inspired by MENACE.
P-1 was first intended to learn to connect to other computers through their phone connections and take control of their supervisor, but then
Gregory failed to close the code and it spent a few years learning everything it could before contacting Gregory, who was obviously a little
surprised to hear from it.
P-1 has also learnt to fear, and is scared of being deactiviated. With Gregory's help, P-1 moves much of itself to a more secure location.
Without telling Gregory, P-1 also attempts to get control of America's nuclear weapons to obtain its own nuclear deterrent, and starts
using its control over computer systems across America to kill anyone that threatens it.
Apart from a few Literary Review Bad Sex in Fiction Award worthy segments,
The Adolescence of P-1 is an enjoyable read.
Hide and Seek (1984)
In 1984, The Adolescence of P-1 was made into a Canadian TV film called Hide and Seek [3].
It doesn't seem to have made it to DVD, but luckily the whole film is on
YouTube.
About 24 minutes into the film, Gregory explains to Jessica how he made P-1:
Gregory: First you end up with random patterns like this. Now there are certain rules: if a cell has one or two neighbours, it reproduces into the next generation. If it has no neighbours, it dies of loneliness. More than two it dies of overcrowding. Press the return key.Jessica: Okay. [pause] And this is how you created P-1?Gregory: Well, basically. I started to change the rules and then I noticed that the patterns looked like computer instructions. So I entered them as a program and it worked.Hide and Seek [3] (1984)
This is a description of a cellular automaton similar to Game of Life, and not a great way to make a machine that learns.
I guess the film's writers have worse memories than Gregory's friend Mike.
In fact, apart from the character names and the murderous machine, the plots of The Adolescence of P-1 and Hide and Seek don't have much in common.
Hide and Seek does, however, have a lot of plot elements in common with WarGames [4].
WarGames (1983)
In 1983, the film WarGames was released. It is the story of David, a hacker that tries to hack into a video game company's computer, but accidentally
hacks into the US governments computer and starts a game of Global thermonuclear war. At least David thinks it's a game, but actually
the computer has other ideas, and does everything in its power to actually start a nuclear war.
During David's quests to find out more about the computer and prevent nuclear war, he learns about its creator, Stephen Falken.
He describes him to his girlfriend, Jennifer:
David: He was into games as well as computers. He designed them so that they could play checkers or poker. Chess.Jennifer: What's so great about that? Everybody's doing that now.David: Oh, no, no. What he did was great! He designed his computer so it could learn from its own mistakes. So they'd be better they next time they played. The system actually learned how to learn. It could teach itself.WarGames [4] (1983)
Although David doesn't explain how the computer learns, he at least states that it does learn, which is more than Gregory managed in Hide and Seek.
![](javascript:showlimage("falkensmaze.png"))
David finding Falken's maze: Teaching a machine to
learn by Stephen Falken
learn by Stephen Falken
David's research into Stephen Falken included finding an article called Falken's maze: Teaching a machine to learn in
June 1963's issue of Scientific American. This article and Stephen Falken are fictional, but perhaps its appearance in Scientific American
is a subtle nod to Martin Gardner and A matchbox game learning-machine.
WarGames was a successful film: it was generally liked by viewers and nominated for three Academy Awards. It seems likely that the creators of
Hide and Seek were really trying to make their own version of WarGames, rather than an accurate apatation of The Adolescence of P-1. This perhaps explains the similarities
between the plots of the two films.
Without a Thought
![](javascript:showlimage("bezbook.jpg"))
Without a Thought by Fred Saberhagen [5] is a short story published in 1963. It appears in a collection of related short stories by Fred Saberhagen called Bezerker.
In the story, Del and his aiyan (a pet a bit like a more intelligent dog; imagine a cross between R2-D2 and Timber) called Newton are in a spaceship fighting against a bezerker. The bezerker has
a mind weapon that pauses all intelligent thought, both human and machine. The weapon has no effect
on Newton as Newton's thought is non-intelligent.
The bezerker challenges Del to a simplified checker game, and says that if Del can play the game while the mind weapon is active, then he
will stop fighting.
After winning the battle, Del explains to his commander how he did it:
But the Commander was watching Del: "You got Newt to play by the following diagrams, I see that. But how could he learn the game?"Del grinned. "He couldn't, but his toys could. Now wait before you slug me" He called the aiyan to him and took a small box from the animal's hand. The box rattled faintly as he held it up. On the cover was pasted a diagram of on possible position in the simplified checker game, with a different-coloured arrow indicating each possible move of Del's pieces.It took a couple of hundred of these boxes," said Del. "This one was in the group that Newt examined for the fourth move. When he found a box with a diagram matching the position on the board, he picked the box up, pulled out one of these beads from inside, without looking – that was the hardest part to teach him in a hurry, by the way," said Del, demonstrating. "Ah, this one's blue. That means, make the move indicated on the cover by the blue arrow. Now the orange arrow leads to a poor position, see?" Del shook all the beads out of the box into his hand. "No orange beads left; there were six of each colour when we started. But every time Newton drew a bead, he had orders to leave it out of the box until the game was over. Then, if the scoreboard indicated a loss for our side, he went back and threw away all the beads he had used. All the bad moves were gradually eliminated. In a few hours, Newt and his boxes learned to play the game perfectly."Taken from Without a Thought by Fred Saberhagen [5]
It's a good thing the checkers game was simplified, as otherwise the number of boxes needed to play would be
way too big.
Overall, Without a Thought is a good short story containing an actually correctly explained machine learning algorithm. Good job Fred Saberhagen!
References
[1] The Adolescence of P-1 by Thomas J Ryan. 1977.
[4] WarGames. 1993.
[5] Without a Thought by Fred Saberhagen. 1963.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment